
分析 (1)由直线l1与直线l2:y=$\frac{1}{3}$x+3平行易得k=$\frac{1}{3}$,设l1解析式为y=$\frac{1}{3}$x+b,将A(2,0)代入解析式,解得b,可得l1表达式;
(2)令x=0,可得直线l1与y轴的交点,利用三角形的面积公式可得结果.
解答 解:(1)∵直线l1与直线l2:y=$\frac{1}{3}$x+3平行,
∴设l1解析式为y=$\frac{1}{3}$x+b,
∵直线l1与x轴的交点的坐标为A(2,0),
∴0=$\frac{1}{3}×2+b$
解得,b=$-\frac{2}{3}$,
∴直线l1的表达式为:y=$\frac{1}{3}x-\frac{2}{3}$;
(2)设直线l1与x轴、y轴的交点的坐标分别为A,B,
令x=0,可得y=$\frac{1}{3}×0-\frac{2}{3}$=$-\frac{2}{3}$,
则B点坐标为(0,-$\frac{2}{3}$)
S△AOB=$\frac{1}{2}$•|OA|•|OB|=$\frac{1}{2}×$2×$\frac{2}{3}$=$\frac{2}{3}$.
直线l1与坐标轴围成的三角形的面积为:$\frac{2}{3}$.
点评 本题主要考查了两直线相交与平行问题,求得直线与两坐标轴的交点坐标是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
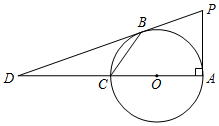 如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$.
如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 进球数n(个) | 0 | 1 | 2 | 3 | 4 | 5 |
| 投进n个球的人数 | 1 | 2 | 7 | 9 | 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com