
| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
分析 (1)①售价-进价即可得;②待定系数法求解可得;
(2)根据总利润=单件利润×销售量,列一元二次方程求解可得;
(3)根据(2)中相等关系列出函数解析式,根据二次函数的性质可得.
解答 解:(1)由题意知销售该图书每本的利润是x-30元,
设月销量m与售价x间的函数关系式为m=kx+b,
由题意得:$\left\{\begin{array}{l}{50k+b=2000}\\{60k+b=1600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-40}\\{b=4000}\end{array}\right.$,
∴月销量m=-40x+4000,
故答案为:①x-30;②-40x+4000;
(2)根据题意可得(x-30)(-40x+4000)=48000,
解得:x=60或x=70,
答:若销售图书的月利润为48000元,则每本图书需要售价60元或70元;
(3)y=(x-30)(-40x+4000)
=-40(x-65)2+49000,
∴售价为65元时,当月的利润最大,最大利润是49000元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式及根据相等关系列出方程或函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
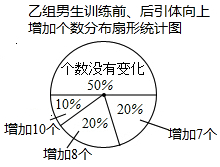 某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.| 甲组 | 男生A | 男生B | 男生C | 男生D | 男生E | 男生F | 平均个数 | 众数 | 中位数 |
| 训练前 | 4 | 6 | 4 | 3 | 5 | 2 | 4 | b | 4 |
| 训练后 | 8 | 9 | 6 | 6 | 7 | 6 | a | 6 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com