
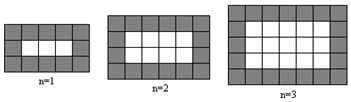
分析 (1)第一个图每一横行有5=1+4个瓷砖,竖列有3=1+2个瓷砖;第二个图每一横行有6=2+4个瓷砖,竖列有4=2+2个瓷砖;第n个图每一横行有n+4个瓷砖,竖列有n+2个瓷砖.
(2)根据(1)中横行和数列的瓷砖数,总数=横行的瓷砖数×竖列的瓷砖数.
(3)根据(2)列的关系式将528代入其中求解.
解答 解:(1)通过观察得:n=1时,横行有1+4块,竖列有1+2块,
n=2时,横行有2+4块,竖列有2+2块,
n=3时,横行有3+4块,竖列有3+2块,
…,
所以在第n个图中,每一横行共有n+4块,每一竖列共有n+2块,
故答案为:n+4,n+2;
(2)由(1)可得总块数可表示为y=(n+4)(n+2);
(3)根据题意可得(n+4)(n+2)=528,
解得:n=20或n=-26,
∴n=20.
点评 此题考查一元二次方程的应用及图形的变化规律,找出图形之间的联系,得出运算规律,利用规律解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 进球数n(个) | 0 | 1 | 2 | 3 | 4 | 5 |
| 投进n个球的人数 | 1 | 2 | 7 | 9 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
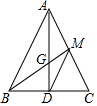 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com