
分析 (1)根据线段垂直平分线的性质得到PA=PB,从而分别表示出PC、BC、BP的长,利用勾股定理列出方程求解即可;
(2)当点P在顶点处时就是在角平分线上,然后再分点P在AC和∠ABC的角平分线的交点处和点P在BC和∠BAC的角平分线的交点处利用相似三角形列式求得t值即可.
解答 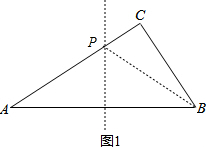 解:(1)如图1,设存在点P,使得PA=PB,
解:(1)如图1,设存在点P,使得PA=PB,
此时PA=PB=2t,PC=4-2t,
在Rt△PCB中,
PC2+CB2=PB2,
即:(4-2t)2+32=(2t)2,
解得:t=$\frac{25}{16}$,
∴当t=$\frac{25}{16}$时,PA=PB;
(2)当点P在点C或点B处时,一定在△ABC的角平分线上,
此时t=2或t=3.5秒;
当点P在∠ABC的角平分线上时,作PM⊥AB于点M,如图2,
此时AP=2t,PC=PM=4-2t,
∵△APM∽△ABC,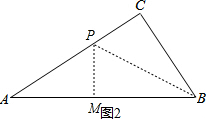
∴AP:AB=PM:BC,
即:2t:5=(4-2t):3,
解得:t=$\frac{5}{4}$;
当点P在∠CAB的平分线上时,作PN⊥AB,如图3,
此时BP=7-2t,PN=PC=(2t-4),
∵△BPN∽△BAC,
∴BP:BA=PN:AC,
即:(7-2t):5=(2t-4):4,
解得:t=$\frac{8}{3}$,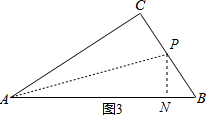
综上,当t=2s或3.5s或$\frac{8}{3}$s或$\frac{5}{4}$s时,点P在△ABC的角平分线上.
点评 本题考查了勾股定理、线段垂直平分线的性质以及角平分线的性质;本题有一定难度,特别是题目的第二问,采用了分类讨论的数学思想,特别是点P与点C和点B重合时的情况很容易遗漏,应该注意.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
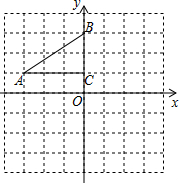 如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(-3,1),B(0,3),C(0,1)
如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(-3,1),B(0,3),C(0,1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com