练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
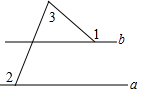
    8．如图，已知直线a∥b，则∠1+∠2-∠3=（　　）
    A．180°B．150°C．135°D．90°

    分析 首先根据平行线的性质得到∠2+∠4=180°，再根据三角形外角的性质即可得到结论．

    解答 解：如图，
    ∵a∥b，
    ∴∠2+∠4=180°，
    ∵∠4=∠5，
    ∴∠2+∠5=180°，
    ∵∠1=∠3+∠5，
    ∴∠1+∠2-∠3=180°，
    故选A．

    点评 本题主要考查了平行线的性质，解题的关键是掌握两直线平行，同位角相等，此题难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．如图，小明在山脚下的A处测得山顶N的仰角为45°，此时，他刚好与山底D在同一水平线上．然后沿着坡度为30°的斜坡正对着山顶前行110米到达B处，测得山顶N的仰角为60°．求山的高度．（结果精确到1米，参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列式子中，正确的是（　　）
    A．-$\sqrt{3.6}$=-0.6B．$\sqrt{36}$=±6C．$\sqrt{（-13）^{2}}$=-13D．$\root{3}{-5}$=-$\root{3}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，将直角三角形ABC沿射线BC的方向平移得到三角形DEF．求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．若一个等腰三角形的两条边的边长之比3：2，则这个等腰三角形底角的正切值为2$\sqrt{2}$或$\frac{\sqrt{7}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

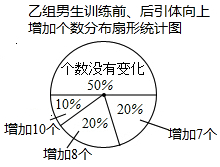    13．某班男生分成甲、乙两组进行引体向上的专项训练，已知甲组有6名男生，并对两组男生训练前，后引体向上的个数进行统计分析，得到乙组男生训练前，后引体向上的平均个数分别是6个和10个，及下面不完整的统计表和图的统计图．
    甲组男生训练前、后引体向上个数统计表（单位：个） 
     甲组 男生A 男生B 男生C 男生D 男生E 男生F 平均个数众数  中位数
     训练前 46 4 3 5 2 4 b  4
     训练后8 9 6 6 7  6 a6c
    （1）根据以上信息，解答下列问题：
    （1）a=7，b=4，c=6.5；
    （2）甲组训练后引体向上的平均个数比训练前增长了75%；
    （3）你认为哪组训练效果好？并提供一个支持你观点的理由；
    （4）小华说他发现了一个错误：“乙组训练后引体向上个数不变的人数占到该组人数的50%，所以乙组的平均个数不可能提高4个之多．：你同意他的观点吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知直线l1与直线l2：y=$\frac{1}{3}$x+3平行，直线l1与x轴的交点的坐标为A（2，0），求：
    （1）直线l1的表达式．
    （2）直线l1与坐标轴围成的三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．阅读下面材料：
    如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=$\frac{k}{x}$交于A（1，3）和B（-3，-1）两点．观察图象可知：当x=-3或1时，y1=y2．
    （1）通过观察函数的图象，可以得到不等式ax+b＞$\frac{k}{x}$的解集x＞1或-3＜x＜0．
    （2）参考观察函数的图象方法，解决问题：关于x的不等式x2+a-$\frac{4}{x}$＜0（a＞0）只有一个整数解，则a的取值范围0＜a＜3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图：矩形纸片ABCD中，AB=4，AD=3折叠纸片．使AD边与对角线BD重合，点A落在点E处，折痕为DG，求AG的长．

    查看答案和解析>>

    同步练习册答案