
分析 作AD⊥BC于点D,则BD=CD=$\frac{1}{2}$BC,分①AB:BC=3:2和②AB:BC=2:3两种情况分别依据等腰三角形性质和勾股定理及正切函数的定义求解可得.
解答 解:如图,作AD⊥BC于点D,
则BD=CD=$\frac{1}{2}$BC,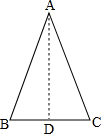
①若AB:BC=3:2,
设AB=3x,则BC=2x,
∴BD=x,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{(3x)^{2}-{x}^{2}}$=2$\sqrt{2}$x,
则tanB=$\frac{AD}{BD}$=$\frac{2\sqrt{2}x}{x}$=2$\sqrt{2}$;
②若AB:BC=2:3,
设AB=2x,则BC=3x,
∴BD=$\frac{3}{2}$x,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{(2x)^{2}-(\frac{3}{2}x)^{2}}$=$\frac{\sqrt{7}}{2}$x,
则tanB=$\frac{AD}{BD}$=$\frac{\frac{\sqrt{7}x}{2}}{\frac{3x}{2}}$=$\frac{\sqrt{7}}{3}$,
故答案为:2$\sqrt{2}$或$\frac{\sqrt{7}}{3}$.
点评 本题主要考查解直角三角形、等腰三角形的性质、勾股定理及三角函数的定义,熟练掌握等腰三角形的性质并据此分类讨论是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
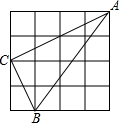 如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
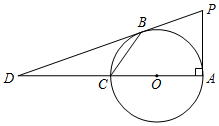 如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$.
如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
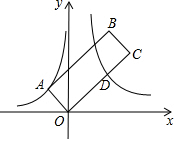 如图,双曲线y=-$\frac{2}{x}$与y=$\frac{6}{x}$分别过矩形ABCO上的A、D两点,OD=2CD,矩形ABCO面积为18$\sqrt{3}$,则OC的长为( )
如图,双曲线y=-$\frac{2}{x}$与y=$\frac{6}{x}$分别过矩形ABCO上的A、D两点,OD=2CD,矩形ABCO面积为18$\sqrt{3}$,则OC的长为( )| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $9\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com