
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)

【答案】(1)AB=![]() 21.2(m)(2)CA=
21.2(m)(2)CA=![]() 略(注意精确度)
略(注意精确度)
【解析】试题分析:(1)首先分析图形:根据题意构造直角三角形,利用在Rt△CPE中,由sin45°=![]() ,得出EC的长度,进而可求出答案.
,得出EC的长度,进而可求出答案.
(2)在Rt△CPE中,tan60°=![]() ,得出BP的长,进而得出PE的长,即可得出答案.
,得出BP的长,进而得出PE的长,即可得出答案.
试题解析:(1)过点C作CE⊥BP于点E,
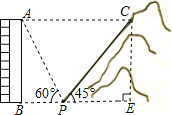
在Rt△CPE中
∵PC=30m,∠CPE=45°,
∴sin45°=![]() ,
,
∴CE=PCsin45°=30×![]() m,
m,
∵点C与点A在同一水平线上,
∴AB=CE=15![]() ≈21.2m,
≈21.2m,
答:居民楼AB的高度约为21.2m;
(2)在Rt△ABP中
∵∠APB=60°,
∴tan60°=![]() ,
,
∴BP=![]() m,
m,
∵PE=CE=15![]() m,
m,
∴AC=BE=15![]() +5
+5![]() ≈33.4m,
≈33.4m,
答:C、A之间的距离约为33.4m.


科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+1向右平移2个单位长度,再向下平移3个长度单位得到的抛物线解析式是( )
A.y=﹣(x﹣2)2+4B.y=﹣(x﹣2)2﹣2
C.y=﹣(x+2)2+4D.y=﹣(x+2)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“妙分线”.
【解决问题】
(1)如图2,若∠MPN= ![]() ,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含
,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含![]() 的代数式表示出所有可能的结果)
的代数式表示出所有可能的结果)
【深入研究】
如图2,若∠MPN=54°,且射线PQ绕点P从PN位置开始,以每秒8°的速度顺时针旋转,当PQ与PN成![]() 时停止旋转,旋转的时间为t秒.
时停止旋转,旋转的时间为t秒.
(2)当t为何值时,射线PM是∠QPN的“妙分线”.
(3)若射线PM同时绕点P以每秒6°的速度顺时针旋转,并与PQ同时停止.请求出当射线PQ 是∠MPN的“妙分线”时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数
B.标准差
C.中位数
D.众数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com