
【题目】如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点.若抛物线y=ax2+bx+4经过A,B,C三点,且AB=6. 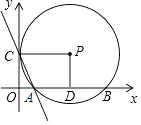
(1)求⊙P的半径R的长;
(2)求该抛物线的解析式;
(3)求出该抛物线与⊙P的第四个交点E的坐标.
【答案】
(1)解:如图1中,连接PA.
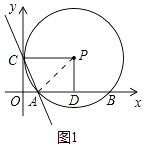
∵PD⊥AB,
∴AD=DB= ![]() AB=3,
AB=3,
∵抛物线y=ax2+bx+4与y轴交于点C,
∴C(0,4),
∴OC=4,
∵四边形PDOC是矩形,
∴PD=OC=3,∠PDA=90°,
∴PC=PA= ![]() =
= ![]() =5,
=5,
∴R=5
(2)解:由(1)可知A(,2,0),B(8,0),
把A、B两点坐标代入y=ax2+bx+4得到, ![]() ,
,
解得 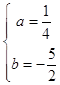 ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+4
x+4
(3)解:如图2中,
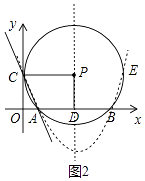
根据对称性,点C、点E关于对称轴x=5对称,
∵点C(0,4)
∴点E坐标(10,4)
【解析】(1)根据垂径定理可得AD=DB=3,在Rt△PAD中,根据PA= ![]() 即可解决问题.(2)先确定A、B两点坐标,再根据待定系数法即可解决问题.(3)根据对称性即可解决问题.
即可解决问题.(2)先确定A、B两点坐标,再根据待定系数法即可解决问题.(3)根据对称性即可解决问题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】第十六届亚远会共颁发金牌477枚,如图是不完整的金牌数条形统计图和扇形统计图, 

根据以上信息.觯答下列问题:
(1)请将条形统计图补充完整;
(2)中国体育健儿在第十六届亚运会上共夺得金牌枚;
(3)在扇形统计图中,日本代表团所对应的扇形的圆心角约为°(精确到1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.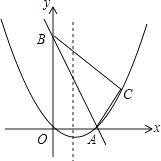
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E,F,连接EF. 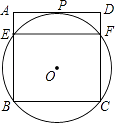
(1)求证:PF平分∠BFD;
(2)若tan∠FBC= ![]() ,DF=
,DF= ![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会求![]() 的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]()
![]()
![]()
(1)由上面的规律我们可以大胆猜想,得到
![]() =________________
=________________
利用上面的结论,求:
(2)![]() 的值。
的值。
(3)求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°. 
(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是正方形ABCD的边CD、AD上的点.且CE=DF,AE、BF相交于点O,下列结论:①AE=BF,②AE⊥BF,③AO=OE,④S△AOB=S四边形DEOF中,错误的有 . (只填序号) 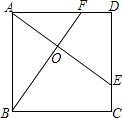
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ![]() ).
).
(1)求点P,Q的坐标;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com