
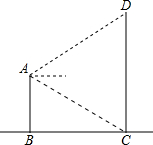
 小明为了测量建筑物CD的高度,在距建筑物CD的水平距离100米的建筑物AB顶上用测角仪得从A点测得D点的仰角为26°36′,从A点测得C点的俯角为63°24′.
小明为了测量建筑物CD的高度,在距建筑物CD的水平距离100米的建筑物AB顶上用测角仪得从A点测得D点的仰角为26°36′,从A点测得C点的俯角为63°24′.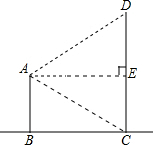 过点A作AE⊥CD于点E,则四边形ABCE为矩形,
过点A作AE⊥CD于点E,则四边形ABCE为矩形,| AB |
| BC |
| ED |
| AE |


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
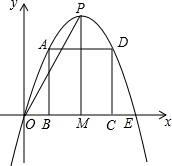 已知抛物线OPE与x轴的交点为点O、点E且OE=4,点A是抛物线OPE的一个动点(不与点O、E重合),作AB⊥X轴于点B,线段AB的最大值是PM=4.
已知抛物线OPE与x轴的交点为点O、点E且OE=4,点A是抛物线OPE的一个动点(不与点O、E重合),作AB⊥X轴于点B,线段AB的最大值是PM=4.查看答案和解析>>
科目:初中数学 来源: 题型:
 探索性问题:
探索性问题:查看答案和解析>>
科目:初中数学 来源: 题型:
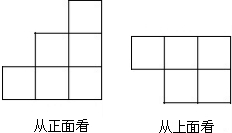 用小立方块搭一个几何体,如图是从正面和上面看到的几何体的形状图,搭成过样的几何体最少需多少个小立方块?最多需要多少个立方块?并画出需要最多立方块时从左面看到的几何体的形状图.
用小立方块搭一个几何体,如图是从正面和上面看到的几何体的形状图,搭成过样的几何体最少需多少个小立方块?最多需要多少个立方块?并画出需要最多立方块时从左面看到的几何体的形状图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com