
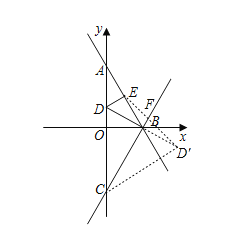
����Ŀ����ͼ��ֱ��y��![]() x+6��y�ύ�ڵ�A����x�ύ�ڵ�B����EΪ�߶�AB���е㣬��ABO��ƽ����BD��y���ཻ�ڵ�D��A��C�������x��Գƣ�
x+6��y�ύ�ڵ�A����x�ύ�ڵ�B����EΪ�߶�AB���е㣬��ABO��ƽ����BD��y���ཻ�ڵ�D��A��C�������x��Գƣ�

��1��һ����P�ӵ�E���������ʵ���·���˶���ֱ��BC�ϵĵ�F�������ʵ���·���˶�����D������P���˶�·�����ʱ�����ʱ��F�����꼰��P�������·���ij���
��2����E��ֱ��y��3ˮƽ�����˶��õ�E'��ƽ�����Ƿ���ڵ�Mʹ����D��B��M��E'Ϊ������ı���Ϊ���Σ������ڣ���ֱ��д����E�������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��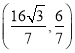 ��2
��2![]() ����2����
����2����![]() ��3����
��3����![]() ��3��
��3��
��������
��1�����ȸ���ֱ����������Ľ�������������꣬Ȼ�����ֱ�������κͽ�ƽ�����Լ��ԳƵ����ʵó���C��D��E�����꣬�����ó�ֱ��BC����ʽ���ٸ��ݶԳ�����ȷ�����·�������ֱ��E��D����ʽ�����������������ɵó���F���ꣻ
��2���������ε����ʣ��������ۣ�BDΪ�ߺ�BDΪ�Խ��ߣ���⼴��.
��1����ֱ��y=![]() x+6��y�ύ�ڵ�A����x�ύ�ڵ�B��
x+6��y�ύ�ڵ�A����x�ύ�ڵ�B��
���A��0��6������B��2![]() ��0����
��0����
�ߵ�EΪ�߶�AB���е㣬
���E��![]() ��3��
��3��
��tan��ABO=![]() ��
��
���ABO=60����
��BDƽ�֡�ABO��
���ABD=��DBO=30������OB=2![]() ��
��
��DO=2��BD=2DO=4
���D��0��2��
��A��C�������x��Գƣ�
���C������0����6��
����ֱ��BC����ʽΪ��y=kx+b��
��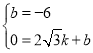
���ã�k=![]() ��b=��6
��b=��6
��ֱ��BC����ʽΪ��y=![]() x��6
x��6
��ͼ������D����ֱ��BC�ĶԳƵ�D'��4![]() ����2��������ED'��BC�ڵ�F��
����2��������ED'��BC�ڵ�F��
���P�������·��ΪD'E�ij���
��D'E=![]() =2
=2![]()
��ֱ��ED'����ʽΪ��y=mx+n��
��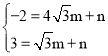
��ã�m=��![]() ��n=
��n=![]()
��ֱ��ED'����ʽΪ��y=��![]() x+
x+![]() ��
��
��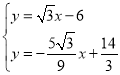
��
���F���꣨![]() ��
��![]() ��
��
��2����BDΪ�ߣ����E'��x��3��
���ı���BDE'M�����Σ�
��BD=DE'=4
��4=![]()
��x=![]() ��
��
���E'��![]() ��3��
��3��
��BDΪ�Խ��ߣ�
���ı���BE'DM������
��DE'=BE'��
�ࣨx��0��2+��3��2��2=��x��2![]() ��2+32��
��2+32��
��x=![]()
���E'���꣨![]() ��3��
��3��
���ϣ���E��������Ϊ��![]() ��3����
��3����![]() ��3��.
��3��.


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ��Щ��ϵ�У����κ���y��ax2+bx��![]() ��ͼ����A����1��0����C��2��0������y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
��ͼ����A����1��0����C��2��0������y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
��1������κ����ı���ʽ���䶥������ꣻ
��2����PΪy���ϵ�һ�����㣬����PD����![]() PB+PD����Сֵ��
PB+PD����Сֵ��
��3��M��x��t��Ϊ�����߶Գ�����һ�����㣬��ƽ���ڴ��ڵ�N��ʹ����A��B��M��NΪ������ı���Ϊ���Σ��������ĵ�N������ ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y����x2+bx+c��ͼ����A����1��0����C��0��3��.
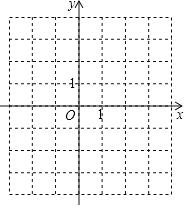
��1������κ����Ľ���ʽ��
��2����ͼ�У��������κ�����ͼ��
��3������ͼ��ֱ��д����y��0ʱ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
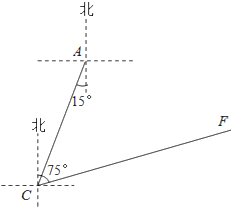
����Ŀ����ͼ����A������ijСѧ����λ��ѧУ��ƫ��15���������120��C�㴦��һ������.ijһʱ��������ͻȻ�ӵ������绰����֪��λ��C�㱱ƫ��75�������F�㴦ͻ�����֣������ӱ���������·��CF�����Ȼ���֪�������ľ����������뾶Ϊ110�ף����������ľ�������ѧУ�Ƿ�����Ӱ�죿�������Ӱ�죬��֪��������ʻ���ٶ�ΪÿСʱ60ǧ�ף����ѧУ��Ӱ��ʱ��Ϊ���룿��![]() ��3.6�������ȷ��1�룩
��3.6�������ȷ��1�룩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
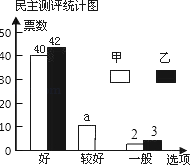
����Ŀ����У���ִ����У��ס�����λͬѧ�ı��ַ���ͻ�����ֳ�A��B��C��D��E��F��λ��ί�Ĵ������Լ������ȡ��50��ͬѧ������������ֱ�����ͳ�Ʊ��Ͳ�����������ͳ��ͼ����˵���������ȡ��50��ͬѧÿ�˱���������������Ϻ�������һ������ѡһƱͶ��ÿ��ѡ�֣�
A | B | C | D | E | F | |
�� | 89 | 97 | 90 | 93 | 95 | 94 |
�� | 89 | 92 | 90 | 97 | 94 | 94 |
��1��a���� ������λ��ί����ͬѧ�����������λ������ ��������ȫ����ͳ��ͼ��
��2��ѧУ�涨���ֱ����£�ȥ����ί��������ߺ���ͷ֣�����ƽ���ֲ���ƽ��������������ְ�2��3�������÷֣���ס�����λͬѧ�����÷֣�����������֣�������Ʊ����2+���Ϻ���Ʊ����1+��һ����Ʊ����0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����E��������ABCD�б�AB���е㣮
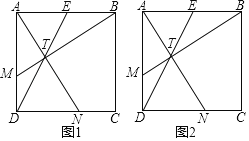
��1����ͼ1����TΪ�߶�DE��һ�㣬����BT���ӳ���AD�ڵ�M������AT���ӳ���CD�ڵ�N����AM��DN�����ж��߶�AN���߶�BM�Ĺ�ϵ����֤������֤����M���߶�AD�Ļƽ�ָ�㣮
��2����ͼ2����AD����ȡһ��M������AM2��DMDAʱ������BM��DE�ڵ�T������AT���ӳ���DC�ڵ�N����tan��MTD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ͼ���һ���֣������ߵ����������A��1��3������
ͼ���һ���֣������ߵ����������A��1��3������![]() ���һ������B��4��0����ֱ��
���һ������B��4��0����ֱ��![]() �������߽���
�������߽���![]() ��
��![]() ���㣬���н��ۣ���
���㣬���н��ۣ���![]() ����
����![]()
![]() ��������
��������![]() ��������ȵ�ʵ����������
��������ȵ�ʵ����������![]() ʱ����
ʱ����![]() ������������
������������![]() �����һ�������ǣ�-1��0����������ȷ���ǣ� ��
�����һ�������ǣ�-1��0����������ȷ���ǣ� ��

A.�٢ڢ�B.�٢ۢ�C.�٢ۢ�D.�ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
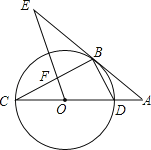
����Ŀ����ͼ��CD����O��ֱ������B����O�ϣ�����BC��BD��ֱ��AB��CD���ӳ����ཻ�ڵ�A��AB2��ADAC��OE��BD��ֱ��AB�ڵ�E��OE��BC�ཻ�ڵ�F��
��1����֤��ֱ��AE����O�����ߣ�
��2������O�İ뾶Ϊ3��cosA��![]() ����OF�ij���
����OF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��������ֱ���
��������ֱ���![]() ��
��![]() ��
��![]() ���㣬����
���㣬����![]() ��
��![]() ��
��
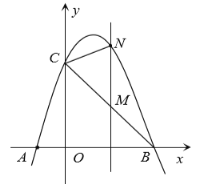
��1��ֱ��д��![]() ��
��![]() ��
��![]() ��������ꣻ
��������ꣻ
��2����![]() ���߶�
���߶�![]() ��һ�㣨����
��һ�㣨����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ��Ĵ��߽��������ڵ�
��Ĵ��߽��������ڵ�![]() ������
������![]() ������
������![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ǡ����
ǡ����![]() ���ϣ������
���ϣ������![]() �����ꣻ
�����ꣻ
��3����ƽ�����Ƿ����һ��![]() ��ʹ
��ʹ![]() ���ڵ�
���ڵ�![]() �ĶԳ�
�ĶԳ�![]() ����
����![]() ��
��![]() ��
��![]() �ֱ��ǵ�
�ֱ��ǵ�![]() ��
��![]() ��
��![]() �ĶԳƵ㣩ǡ���������������ڸ��������ϣ������ڣ������
�ĶԳƵ㣩ǡ���������������ڸ��������ϣ������ڣ������![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com