
����Ŀ����ͼ����ƽ��ֱ��Щ��ϵ�У����κ���y��ax2+bx��![]() ��ͼ����A����1��0����C��2��0������y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
��ͼ����A����1��0����C��2��0������y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
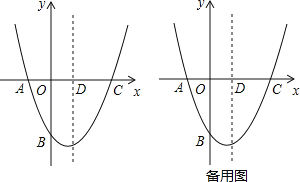
��1������κ����ı���ʽ���䶥������ꣻ
��2����PΪy���ϵ�һ�����㣬����PD����![]() PB+PD����Сֵ��
PB+PD����Сֵ��
��3��M��x��t��Ϊ�����߶Գ�����һ�����㣬��ƽ���ڴ��ڵ�N��ʹ����A��B��M��NΪ������ı���Ϊ���Σ��������ĵ�N������ ������
���𰸡���1��![]() �������ߵĶ�������Ϊ��
�������ߵĶ�������Ϊ��![]() ������2����СֵΪ
������2����СֵΪ![]() ����3��5��
����3��5��
��������
(1)��A��C������������y=ax2+bx��![]() �����ô���ϵ��������������κ����ı���ʽ�������õ��䶥�����ꣻ
�����ô���ϵ��������������κ����ı���ʽ�������õ��䶥�����ꣻ
(2)����AB����DH��AB��H����OB��P����ʱ![]() PB+PD��С����Сֵ�����߶�DH�����DH���ɣ�
PB+PD��С����Сֵ�����߶�DH�����DH���ɣ�
(3)����A��B��M��NΪ������ı���Ϊ����ʱ�����������������AΪԲ��ABΪ�뾶������Գ������������㣬��ʱAM=AB������BΪԲ��ABΪ�뾶������Գ������������㣬��ʱBM=AB�����߶�AB�Ĵ�ֱƽ������Գ�����һ�����㣬��ʱAM=BM����M��ĸ�����ɵó���N�ĸ�����5����
(1)�߶��κ���![]() ��ͼ����A(��1��0)C(2��0)��
��ͼ����A(��1��0)C(2��0)��
�� ��
��
��ã� ��
��
����κ����ı���ʽΪ![]() ��
��
��y=![]() ��
��
�������ߵĶ�������Ϊ(![]() )��
)��
(2)��ͼ������AB����DH��AB��H����OB��P����ʱ![]() PB+PD��С��
PB+PD����

���ɣ���OA=1��OB=![]() ��
��
��![]() ��
��
��![]() ��
��
���ABO=30����
��PH=![]() PB��
PB��
��![]() PB+PD=PH+PD=DH��
PB+PD=PH+PD=DH��
���ʱ![]() PB+PD���(���߶����);
PB+PD���(���߶����);
�������ߵĶ�������Ϊ(![]() )��
)��
��![]() ��
��
�ߡ�ABO=30����
���HAD=60����
��Rt��ADH�У��ߡ�AHD=90����AD=![]() ����HAD=60����
����HAD=60����
��sin60��=![]() ��
��
��DH=![]() ��
��
��![]() PB+PD����СֵΪ
PB+PD����СֵΪ![]() ��
��
(3)����AΪԲ��ABΪ�뾶��������ΪAB��AD���ʴ�ʱԲ����Գ������������㣬��AM=AB����M�������������������������N����������
����BΪԲ��ABΪ�뾶��������Ϊ![]() ���ʴ�ʱԲ����Գ������������㣬��BM=AB����M������������������������N����������
���ʴ�ʱԲ����Գ������������㣬��BM=AB����M������������������������N����������
���߶�AB�Ĵ�ֱƽ������Գ�����һ�����㣬��ʱAM=BM����ΪM����һ������������������N����һ����
������������N�㹲��5����
�ʴ�Ϊ��5��


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
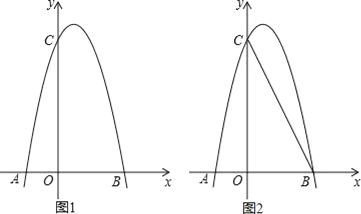
����Ŀ����ͼ1���Գ���Ϊֱ��x=![]() �������߾���B��2��0����C��0��4�����㣬��������x�����һ����ΪA
�������߾���B��2��0����C��0��4�����㣬��������x�����һ����ΪA
��1���������ߵĽ���ʽ��
��2������PΪ��һ�������������ϵ�һ�㣬���ı���COBP�����ΪS����S�����ֵ��
��3����ͼ2����M���߶�BC��һ���㣬��x���Ƿ���������ĵ�Q��ʹ��MQCΪ��������������MQBΪֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC�У��ױ�BC��Ϊ8������Ϊ6����D��BC����һ�㣬����B��AC��ƽ�������A��B��D�����Բ���ڵ�E������DE����DE����Сֵ��___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����ABΪֱ������O��BC�ڵ�D������D��AC�Ĵ��߽�AC�ڵ�E����AB���ӳ����ڵ�F��

��1����֤��DE����O���У�
��2����CD��BF��AE��3����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̻����Ӧ���⣺
ȥ�����ڣ�ij�����ڱ��굼�µ�·�жϣ��õع������֯�繤�������ޣ�����־���������15ǧ�ף�����װ������������ȴӹ���ֳ�����10���Ӻ繤�˼��ճ���ͬһ�ص�������������ͬʱ���������أ���֪���ճ��ٶ��������ٶȵ�1.5�������ճ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �У�AB=8��BC=6�����Խ���
�У�AB=8��BC=6�����Խ���![]() �е�
�е�![]() ��ֱ�߷ֱ�
��ֱ�߷ֱ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() .
.

(1)��֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
(2)���ı���![]() ������ʱ����
������ʱ����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��3x��0��
�⣺x(x��3)��0��
��![]() ��
��![]() ��
��
���x��3��x��0��
��һԪ���β���ʽx2��3x��0�Ľ⼯Ϊx��0��x��3��
�������������̻ش��������⣺
��1�������������������ѧ˼��Ϊ����������
��2��һԪ���β���ʽx2��3x��0�Ľ⼯Ϊ����������
��3���������Ƶķ�����һԪ���β���ʽ��x2��2x��3��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��![]() x2��bx��c����A(3, 0)����B(0, 3)����M(m, 0)���߶�OA�ϣ����A��O���غϣ�������M��x��Ĵ������߶�AB���ڵ�P���������߽��ڵ�Q������BQ��
x2��bx��c����A(3, 0)����B(0, 3)����M(m, 0)���߶�OA�ϣ����A��O���غϣ�������M��x��Ĵ������߶�AB���ڵ�P���������߽��ڵ�Q������BQ��
��1���������߱���ʽ��
��2������OP������BOP����PBQʱ����PQ�ij��ȣ�
��3������PBQΪ����������ʱ����m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+6��y�ύ�ڵ�A����x�ύ�ڵ�B����EΪ�߶�AB���е㣬��ABO��ƽ����BD��y���ཻ�ڵ�D��A��C�������x��Գƣ�
x+6��y�ύ�ڵ�A����x�ύ�ڵ�B����EΪ�߶�AB���е㣬��ABO��ƽ����BD��y���ཻ�ڵ�D��A��C�������x��Գƣ�

��1��һ����P�ӵ�E���������ʵ���·���˶���ֱ��BC�ϵĵ�F�������ʵ���·���˶�����D������P���˶�·�����ʱ�����ʱ��F�����꼰��P�������·���ij���
��2����E��ֱ��y��3ˮƽ�����˶��õ�E'��ƽ�����Ƿ���ڵ�Mʹ����D��B��M��E'Ϊ������ı���Ϊ���Σ������ڣ���ֱ��д����E�������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com