
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.

(1)求证:DE与⊙O相切;
(2)若CD=BF,AE=3,求DF的长.
【答案】(1)见解析;(2)DF=2![]() .
.
【解析】
(1)连接OD,求出AC∥OD,求出OD⊥DE,根据切线的判定得出即可;
(2)求出∠1=∠2=∠F=30°,求出AD=DF,解直角三角形求出AD,即可求出答案.
(1)证明:连接OD,

∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵AB=AC,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠ADO,
∴∠1=∠ADO,
∴OD∥AC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∴OD⊥ED,
∵OD过O,
∴DE与⊙O相切;
(2)解:∵AB=AC,AD⊥BC,
∴∠1=∠2,CD=BD,
∵CD=BF,
∴BF=BD,
∴∠3=∠F,
∴∠4=∠3+∠F=2∠3,
∵OB=OD,
∴∠ODB=∠4=2∠3,
∵∠ODF=90°,
∴∠3=∠F=30°,∠4=∠ODB=60°,
∵∠ADB=90°,
∴∠2=∠1=30°,
∴∠2=∠F,
∴DF=AD,
∵∠1=30°,∠AED=90°,
∴AD=2ED,
∵AE2+DE2=AD2,AE=3,
∴AD=2![]() ,
,
∴DF=2![]() .
.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有![]() 个质地、大小均相同的小球,这些小球分别标有数字
个质地、大小均相同的小球,这些小球分别标有数字![]() ,甲、乙两人每次同时从袋中各随机摸出
,甲、乙两人每次同时从袋中各随机摸出![]() 个球,并计算摸出的这
个球,并计算摸出的这![]() 个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表
个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表
摸球总次数 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
解答下列问题:
![]() 如果实验继续进行下去,根据上表数据,出现“和为
如果实验继续进行下去,根据上表数据,出现“和为![]() ”的频率将稳定在它的概率附近.估计出现“和为
”的频率将稳定在它的概率附近.估计出现“和为![]() ”的概率是_______;
”的概率是_______;
![]() 如果摸出的这两个小球上数字之和为
如果摸出的这两个小球上数字之和为![]() 的概率是
的概率是![]() ,那么
,那么![]() 的值可以取
的值可以取![]() 吗?请用列表法或画树状图法说明理由;如果
吗?请用列表法或画树状图法说明理由;如果![]() 的值不可以取
的值不可以取![]() ,请写出一个符合要求的
,请写出一个符合要求的![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
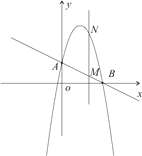
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角三角形ABC内接于⊙O(AB>AC),AD⊥BC于点D,BE⊥AC于点E,AD、AE交于点F.
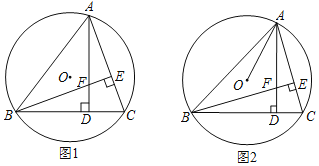
(1)如图1,若⊙O直径为10,AC=8,求BF的长;
(2)如图2,连接OA,若OA=FA,AC=BF,求∠OAD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是( )

A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5
查看答案和解析>>
科目:初中数学 来源: 题型:
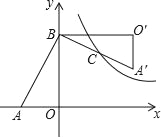
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角些标系中,二次函数y=ax2+bx﹣![]() 的图象经过点A(﹣1,0),C(2,0),与y轴交于点B,其对称轴与x轴交于点D.
的图象经过点A(﹣1,0),C(2,0),与y轴交于点B,其对称轴与x轴交于点D.
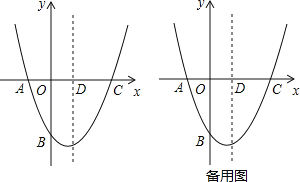
(1)求二次函数的表达式及其顶点的坐标;
(2)若P为y轴上的一个动点,连接PD,求![]() PB+PD的最小值;
PB+PD的最小值;
(3)M(x,t)为抛物线对称轴上一个动点,若平面内存在点N,使得以A、B、M、N为顶点的四边形为菱形,则这样的点N共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤![]()
正确的有( )
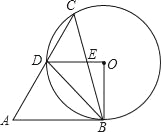
A. ①② B. ①④⑤ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
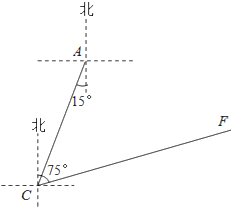
【题目】如图,点A是我市某小学,在位于学校南偏西15°方向距离120米的C点处有一消防车.某一时刻消防车突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即沿路线CF赶往救火.已知消防车的警报声传播半径为110米,问消防车的警报声对学校是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对学校的影响时间为几秒?(![]() ≈3.6,结果精确到1秒)
≈3.6,结果精确到1秒)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com