
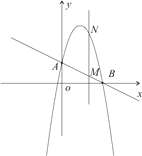
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
【答案】(1)![]() ;
;
(2) 当t=2时,MN的最大值是4.
【解析】试题分析:(1)求出点A、点B的坐标,将A、B坐标代入抛物线解析式,求出b、c的值即可;(2)将M、N的坐标用含t的式子表示,然后将MN表示为二次函数的形式,求二次函数最值即可.
试题解析:
(1)易得A(0,2),B(4,0),
将x=0,y=2代入y=-x2+bx+c得c=2,
将x=4,y=0 代入y=-x2+bx+2,得-16+4b+2=0,解得b=![]() ,
,
∴抛物线解析式为y=-x2+![]() x+2;
x+2;
(2)由题意易得M(t,- ![]() t+2),N(t,-t2+
t+2),N(t,-t2+![]() t+2),
t+2),
∴MN=-t2+![]() t+2-(-
t+2-(-![]() t+2)=-t2+
t+2)=-t2+![]() t+2+
t+2+![]() t-2=-t2+4t=-(t-2)2+4,
t-2=-t2+4t=-(t-2)2+4,
∴当t=2时,MN有最大值4.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,在第一象限内有一动点
,在第一象限内有一动点![]() 在反比例函数
在反比例函数![]() 上,由点
上,由点![]() 向
向![]() 轴,
轴,![]() 轴所作的垂线
轴所作的垂线![]() ,
,![]() (垂足为
(垂足为![]() ,
,![]() )分别与直线
)分别与直线![]() 相交于点
相交于点![]() ,点
,点![]() ,当点
,当点![]() 运动时,矩形
运动时,矩形![]() 的面积为定值
的面积为定值![]() .
.

(1)求![]() 的度数;
的度数;
(2)求反比例函数解析式.
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且AF=FC,GH⊥CD于H.下列说法①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH∶∠ECH=2∶7,则∠EGH=40°.其中正确的有________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]()
(1)请直接写出方程![]() 的所有正整数解
的所有正整数解
(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
查看答案和解析>>
科目:初中数学 来源: 题型:
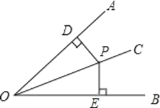
【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,OC是∠AOB的角平分线,点 P 在 OC 上, 求证: .
(要求:请你补全已知和求证,并写出证明过程.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:0,-3.14,-(-10),![]() ,-4
,-4![]() ,15%,
,15%,![]() ,0.3,
,0.3,![]() ,10.01001000100001…
,10.01001000100001…
非负整数集合:{ …}
正分数集合:{ …}
无理数集合:{ …}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com