
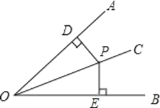
【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,OC是∠AOB的角平分线,点 P 在 OC 上, 求证: .
(要求:请你补全已知和求证,并写出证明过程.)
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)﹣(﹣2)+(﹣4);
(2)﹣10+14+16﹣8;
(3)(-4)×(-5)-90÷(-15);
(4)﹣23÷![]() ×(﹣
×(﹣![]() )2;
)2;
(5)(![]() +
+![]() ﹣
﹣![]() )×(﹣36);
)×(﹣36);
(6)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
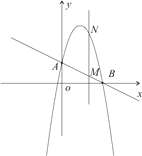
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
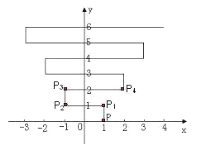
【题目】如下图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位…,依此规律跳动下去,点P第2019次跳动至点P2019的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)在数轴上表示下列各数:0,–2.5,![]() ,–2,+5,
,–2,+5,![]() .
.
![]()
(2)将上列各数用“<”连接起来:___________ _____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com