
【题目】如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且AF=FC,GH⊥CD于H.下列说法①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH∶∠ECH=2∶7,则∠EGH=40°.其中正确的有________.

【答案】①②③④.
【解析】
灵活利用平行线的性质、等角的余角相等、四边形的内角和、三角形内角和定理、三角形的面积公式、角平分线的性质进行分析.
解:①中,根据两条直线平行,同旁内角互补,得∠BAC+∠ACD=180°,
再根据角平分线的概念,得∠GAC+∠GCA=![]() ∠BAC+
∠BAC+![]() ∠ACD=
∠ACD=![]() ×180°=90°,
×180°=90°,
再根据三角形的内角和是180°,得AG⊥CG;
②中,根据等角的余角相等,得∠CGE=∠GAC,故∠BAG=∠CGE;
③中,根据三角形的面积公式,
∵AF=CF,∴S△AFG=S△CFG;
④中,根据题意得:在四边形GECH中,∠EGH+∠ECH=180°.
又∠EGH:∠ECH=2:7,则∠EGH=180°×![]() =40°.
=40°.
故上述四个都是正确的.
故答案为:①②③④.


科目:初中数学 来源: 题型:
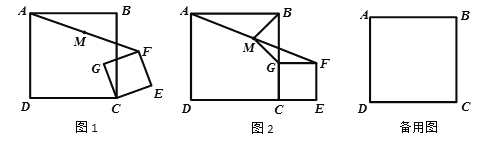
【题目】如图1,正方形CEFG绕正方形ABCD的顶点C旋转,连接AF,点M是AF中点.
(1)当点G在BC上时,如图2,连接BM、MG,求证:BM=MG;
(2)在旋转过程中,当点B、G、F三点在同一直线上,若AB=5,CE=3,则MF= ;
(3)在旋转过程中,当点G在对角线AC上时,连接DG、MG,请你画出图形,探究DG、MG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)﹣(﹣2)+(﹣4);
(2)﹣10+14+16﹣8;
(3)(-4)×(-5)-90÷(-15);
(4)﹣23÷![]() ×(﹣
×(﹣![]() )2;
)2;
(5)(![]() +
+![]() ﹣
﹣![]() )×(﹣36);
)×(﹣36);
(6)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更有效地开展“线上教学”工作,某市就学生参与线上学习的工具进行了电子问卷调查,并将调查结果绘制成图1和图2所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:

(1)本次调查的总人数是 人;
(2)请将条形统计图补充完整;
(3)在扇形统计图中表示观点B的扇形的圆心角度数为 度;
(4)在扇形统计图中表示观点E的百分比是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
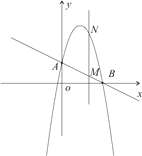
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
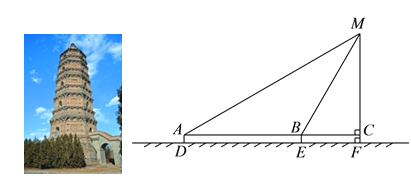
【题目】某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点![]() 用高
用高![]() 米的测角仪
米的测角仪![]() 测得塔顶
测得塔顶![]() 的仰角为
的仰角为![]() ,然后沿
,然后沿![]() 方向前行
方向前行![]() m到达点
m到达点![]() 处,在
处,在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() .请根据他们的测量数据求此塔
.请根据他们的测量数据求此塔![]() 的高.(结果精确到
的高.(结果精确到![]() m,参考数据:
m,参考数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com