
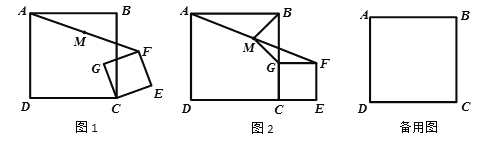
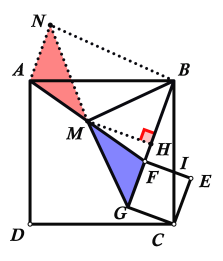
【题目】如图1,正方形CEFG绕正方形ABCD的顶点C旋转,连接AF,点M是AF中点.
(1)当点G在BC上时,如图2,连接BM、MG,求证:BM=MG;
(2)在旋转过程中,当点B、G、F三点在同一直线上,若AB=5,CE=3,则MF= ;
(3)在旋转过程中,当点G在对角线AC上时,连接DG、MG,请你画出图形,探究DG、MG的数量关系,并说明理由.
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)DG=
;(3)DG=![]() MG,理由见解析.
MG,理由见解析.
【解析】
(1)连接MG并延长交AB于N点,证明△ANM≌△FGM后得到MG=MN,AN=CG,进而得到BN=BG,得到△ANG为等腰直角三角形,即可证明MG=MB.
(2)分两种情况画出图形再利用(1)中的思路结合勾股定理即可求解.
(3)先画出图形,然后证明△ADG≌△ABG,得到DG=BG,又△BMG为等腰直角三角形,故而得到DG=BG=![]() MG.
MG.
解:(1) 连接MG并延长交AB于N点,如下图所示:
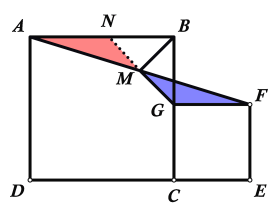
∵GF∥AN,
∴∠NAM=∠GFM
在△ANM和△FGM中
 ,∴△ANM≌△FGM(ASA)
,∴△ANM≌△FGM(ASA)
∴MG=MN,CG=GF=AN
∴AB-AN=BC-CG
∴NB=GB
∴△NBG为等腰直角三角形
又M是NG的中点
∴由直角三角形斜边上的中线等于斜边的一半知:
故有:MG=MB.
(2)分类讨论:
情况一:当B、G、F三点在正方形ABCD外同一直线上时

延长MG到N点,并使得MG=MN,连接AN,BN
∴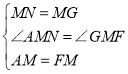 ,∴△AMN≌△FMG(SAS)
,∴△AMN≌△FMG(SAS)
∴AN=GF=GC,∠NAM=∠GFM
∴AN∥GF
∴∠NAB+∠ABG=180°
又∠ABC=90°
∴∠NAB+∠CBG=90°
又在△BCG中,∠BCG+∠CBG=90°
∴∠NAB=∠BCG
∴在△ABN中和△CBG中: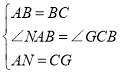 ,∴△ABN≌△CBG(SAS)
,∴△ABN≌△CBG(SAS)
∴BN=BG,∠ABN=∠CBG
∴∠ABC=∠NBG=90°
∴△NBG是等腰直角三角形,且∠BGN=45°
在Rt△BCG中,![]()
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形
∴MH=BH=HG=![]() BG=2
BG=2
在Rt△MFH中,![]()
情况二:当B、G、F三点在正方形ABCD内同一直线上时
如下图所示,延长MG到MN,并使得MG=MN,连接NA、NB,
同情况一中证明思路,
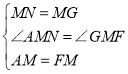 ,△AMN≌△FMG(SAS)
,△AMN≌△FMG(SAS)
∴AN=GF=GC,∠NAM=∠GFM
∴AN∥GF
∴∠NAB=∠ABG
又∠ABG+∠GBC=90°
∠GBC+∠BIF=90°
∴∠BIF=∠ABG
又∠BIF=∠BCG,∠ABC=∠NAB
∴∠NAB=∠GCB
∴在△ABN中和△CBG中: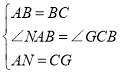 ,∴△ABN≌△CBG(SAS)
,∴△ABN≌△CBG(SAS)
∴BN=BG,∠ABN=∠CBG
∴∠ABC=∠NBG=90°
∴△NBG是等腰直角三角形,且∠BGN=45°
在△BCG中,![]()
过M点作MH⊥BG于H点,∴△MHB为等腰直角三角形
∴MH=BH=HG=![]() BG=2
BG=2
∴HF=HG-GF=2-1=1
在Rt△MFH中,![]()
故答案为:![]() 或
或![]()
(3)由题意作出图形如下所示:
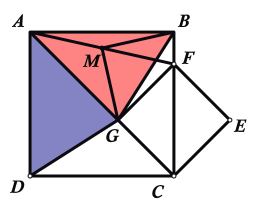
DG、MG的数量关系为:DG=![]() MG,理由如下:
MG,理由如下:
∵G点在AC上
∴∠DAG=∠BAG=45°
在△ADG和△ABG中:
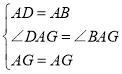 ,∴△ADG≌△BAG(SAS)
,∴△ADG≌△BAG(SAS)
∴DG=BG
又由(2)中的证明过程可知:△MBG为等腰直角三角形
∴BG=![]() MG
MG
∴DG=![]() MG
MG
故答案为:DG=![]() MG.
MG.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
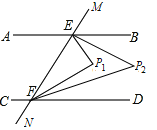
【题目】如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A:国学诵读”,“B:演讲”,“C:课本剧”,“D:书法”.每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如图所示:

(1) 此次一共抽取 名学生进行统计调查;扇形统计图中,活动D所占圆心角为 °;
(2) 请补全条形统计图;
(3) 学校共有720名学生希望参加活动A,试估算该校共有多少名学生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防疾病,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量![]() (mg)与燃烧时间
(mg)与燃烧时间![]() (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后, ![]() 与
与![]() 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时![]() 与
与![]() 的函数关系式.(2)求药物燃烧后
的函数关系式.(2)求药物燃烧后![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
, ![]() .且点
.且点![]() 横坐标是点
横坐标是点![]() 纵坐标的2倍.
纵坐标的2倍.
(1)求反比例函数的解析式;
(2)设点![]() 横坐标为
横坐标为![]() ,
, ![]() 面积为
面积为![]() ,
,
求![]() 与
与![]() 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
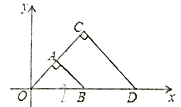
【题目】如图,△OAB与△OCD是以点0为位似中心的位似图形,相似比为1:2,∠OCD=90![]() ,CO=CD.若B(2,0),则点C的坐标为( )
,CO=CD.若B(2,0),则点C的坐标为( )
A. (2,2) B. (1,2) C. (![]() ,2
,2![]() ) D. (2,1)
) D. (2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且AF=FC,GH⊥CD于H.下列说法①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH∶∠ECH=2∶7,则∠EGH=40°.其中正确的有________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com