
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;进球数的中位数为 个,众数为 个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).
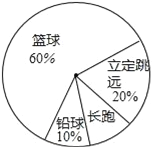
【答案】(1)5,5,4;(2)40;(3)4.2个
【解析】试题分析:(1)根据:人均进球数=![]() ,求解即可;将数据按照从小到大的顺序排列,根据中位数和众数的概念求解;
,求解即可;将数据按照从小到大的顺序排列,根据中位数和众数的概念求解;
(2)根据选择篮球的学生人数和选择篮球的学生人数所占全班人数的百分比,求解即可;
(3)设参加训练之前的人均进球数为x个,然后根据题意列出方程求解即可.
解:(1)人均进球数=![]() =
=![]() =5(个);
=5(个);
根据中位数的概念,由图表可得出第12和第13名学生的进球数均为5个,故进球数的中位数为![]() =5(个),
=5(个),
从图表可以看出进球数为4个的学生人数最多,故进球数的众数为4个,
故训练后篮球定时定点投篮人均进球数为5个;进球数的中位数为5个,众数为 4个;
(2)全班学生的总人数为:24÷60%=40(人);
答:该班共有40个学生.
(3)设参加训练之前的人均进球数为x个,
则有:x(1+20%)=5,
解得:x=4.2.
答:参加训练之前的人均进球数为4.2个.


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.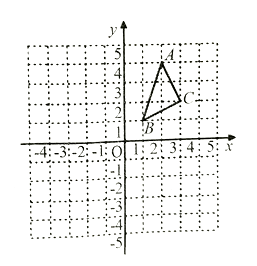
①作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;②在y轴上找点D,使得AD+BD最小,作出点D并写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜.
(1)用树状图或列表法求小华、小丽获胜的概率;
(2)这个游戏规则对双方公平吗?请判断并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B(2,0)两点(点A在点B的左侧),与y轴交于点C(0,8).
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位长度,使平移后所得抛物线的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)已知点Q在x轴上,点P在抛物线上,是否存在以A、C、P、Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
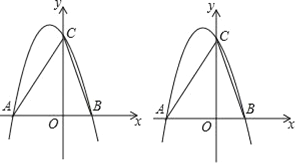
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() .如图
.如图![]() ,正方形
,正方形![]() 的顶点
的顶点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在第二象限.现将正方形
在第二象限.现将正方形![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得到正方形
得到正方形![]() .
.
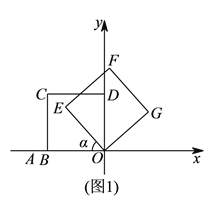

(![]() )如图
)如图![]() ,若
,若![]() ,
, ![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.
(![]() )若
)若![]() 为锐角,
为锐角, ![]() ,当
,当![]() 取得最小值时,求正方形
取得最小值时,求正方形![]() 的面积.
的面积.
(![]() )当正方形
)当正方形![]() 的顶点
的顶点![]() 落在
落在![]() 轴上时,直线
轴上时,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
, ![]() 的其中两边之比能否为
的其中两边之比能否为![]() ?若能,求出
?若能,求出![]() 的坐标;若不能,试说明理由.
的坐标;若不能,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com