
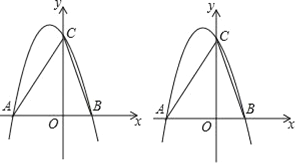
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B(2,0)两点(点A在点B的左侧),与y轴交于点C(0,8).
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位长度,使平移后所得抛物线的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)已知点Q在x轴上,点P在抛物线上,是否存在以A、C、P、Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+8;(2)3<m<9;(3)满足条件的点Q为(﹣2,0)或(﹣6,0)或(3+![]() ,0)或(3﹣
,0)或(3﹣![]() ,0).
,0).
【解析】试题分析:(1)把点B和点C的坐标代入抛物线的解析式得到关于b、c的方程组,从而可求得b、c的值,然后可得到抛物线的解析式;
(2)平移后抛物线的解析式为y=﹣(x+1)2+9﹣m,然后求得直线AC的解析式y=2x+8,当x=﹣1时,y=6,最后由抛物线的顶点在△ABC的内部可得到0<9﹣m<6,从而可求得m的取值范围;
(3)设点Q的坐标为(a,0),点P(x,y).分为AC为对角线、CP为对角线、AQ为对角线三种情况,依据平行四边形对角相互平分的性质和中点坐标公式可求得x、y的值(用a的式子表示),然后将点P的坐标代入抛物线的解析式可求得a的值,从而可得到点Q的坐标.
试题解析:(1)把点B和点C的坐标代入抛物线的解析式得: ![]() ,解得:
,解得: ![]() ,
,
∴y=﹣x2﹣2x+8.
(2)y=﹣x2﹣2x+8=﹣(x+1)2+9,
∴平移后抛物线的解析式为y=﹣(x+1)2+9﹣m.
∵抛物线的对称轴为x=﹣1,点B(2,0),
∴A(﹣4,0).
设直线AC的解析式为y=kx+8,将点A的坐标代入得:﹣4k+8=0,解得k=2,
∴直线AC解析式为y=2x+8.
当x=﹣1时,y=6.
∵抛物线的顶点落在△ABC的内部,
∴0<9﹣m<6.
∴3<m<9.
(3)设点Q的坐标为(a,0),点P(x,y).
①当AC为对角线时.
∵四边形APCQ为平行四边形,
∴AC与PQ互相平分.
依据中点坐标公式可知: ![]() =
=![]() ,
, ![]() .
.
∴x=﹣4﹣a,y=8.
∵点P在抛物线上,
∴﹣(a+4)2﹣2(﹣4﹣a)=0,解得:a=﹣2或a=﹣4(舍去)
∴点P的坐标为(﹣2,0).
②当CP为对角线时,
∵四边形APCQ为平行四边形,
∴CP与AQ互相平分.
依据中点坐标公式可知: ![]() ,
, ![]() ,
,
∴x=a+4,y=8.
∵点P在抛物线上,
∴﹣(a+4)2﹣2(a+4)=0,解得:a=﹣6或a=﹣4(舍去)
∴点P的坐标为(﹣6,0).
③AQ为对角线时.
∵四边形APCQ为平行四边形,
∴AQ与CP互相平分.
依据中点坐标公式可知: ![]() ,
, ![]() ,
,
∴x=﹣4+a,y=﹣8.
∵点P在抛物线上,
∴﹣(a﹣4)2﹣2(a﹣4)+16=0,整理得:a2﹣6a﹣8=0,解得:a=3+![]() 或a=3﹣
或a=3﹣![]() .
.
∴点Q的坐标为(3+![]() ,0)或(3﹣
,0)或(3﹣![]() ,0).
,0).
综上所述满足条件的点Q为(﹣2,0)或(﹣6,0)或(3+![]() ,0)或(3﹣
,0)或(3﹣![]() ,0).
,0).


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
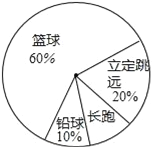
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;进球数的中位数为 个,众数为 个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线l上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1 + S2 +S3 +S4 = . 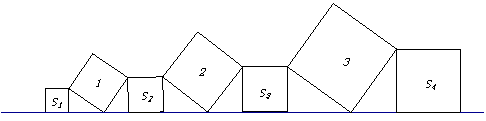
查看答案和解析>>
科目:初中数学 来源: 题型:
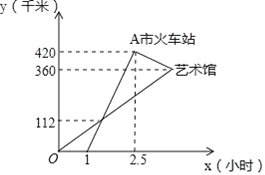
【题目】高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离开N市的距离y与乘车时间x的函数关系式;
(3)若甲要提前30分钟到达艺术馆,那么私家车的速度必须达到多少千米/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
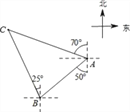
A. 10![]() 海里 B. 10
海里 B. 10![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com