
【题目】如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为144,则BE________

【答案】12
【解析】
作BF⊥CD交CD的延长线于点F,由已知条件可证得∠ABE=∠CBF,且由已知∠AEB=∠CFB=90°,AB=BC,所以△ABE≌△CBF,可得BE=BF,四边形ABCD的面积等于新正方形FBED的面积,即可得BE长.
过B点作BF⊥CD,与DC的延长线交于F点,则∠F=90°,

∵BE⊥AD,∴∠AEB=∠BED=90°,
又∵∠CDA=90°,
∴四边形BEDF是矩形,
∴∠EBF=90°,
∵∠ABC=90°,
∴∠ABE+∠EBC=∠CBF+∠EBC,
∴∠ABE=∠CBF,
又AB=BC,
∴△ABE≌△CBF,
∴BE=BF,
∴矩形BEDF为正方形,
∴S正方形BEDF=S△BCF+S四边形BEDC= S△BAE+S四边形BEDC=S四边形ABCD=144,
∴BE2=144,
∴BE=12,
故答案为:12.


科目:初中数学 来源: 题型:
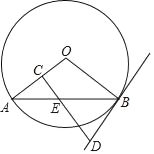
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且![]() ),则称点P′为点P的“k属派生点”.例如:P(1,4)属派生点为P′(1+2×4,2×1+4),即P′(9,6).
),则称点P′为点P的“k属派生点”.例如:P(1,4)属派生点为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-2,3)的“2属派生点”P′的坐标为__________.
(2) 若点P的“3属派生点”P′的坐标为(6,2),求点P的坐标;
(3) 若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
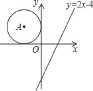
【题目】如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x﹣4上,则⊙A的半径为( )
A. ![]() B. 2 C. 4 D. 6
B. 2 C. 4 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A为线段BC外一动点,且BC=4,AB=3,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.

(1)请找出图中与BE相等的线段,并说明理由;
(2)当∠ABC=30°时,求线段BE长;
(3)直接写出线段BE长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:

如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是___________;
(2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以线段AB两端点A,B为圆心,以大于![]() AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
(1)判断四边形ACBD的形状,并说明理由;
(2)求证:ME=AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A>∠B,分别以点A,C为圆心,大于![]() AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于
AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于![]() BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com