
分析 分析:把方程①中用平方法转化为两个二元一次方程x-y=3或x-y=-3,方程②用因式分解法转化为两个二元一次方程x+y-2=0或x+y-3=0,最后原方程组转化为四个二元一次方程组来求解.
解答 解:由方程①得x-y=±3,
∴x-y=3或x-y=-3
由方程②,得(x+y-2)(x+y-3)=0,
∴x+y-2=0或x+y-3=0,
∴原方程组可化为$\left\{\begin{array}{l}{x-y=3}\\{x+y-2=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-y=3}\\{x+y-3=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-y=-3}\\{x+y-2=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-y=-3}\\{x+y-3=0}\end{array}\right.$.
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{5}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$
点评 本题考查了高次方程.关键是将方程组中的某个方程左边因式分解,使其积为0或两边开平方,可将较复杂的高次方程组转化为简单的高次方程组或者一次方程组来求解.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
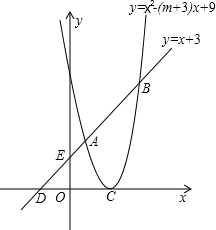 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com