
【题目】请将下列事件发生的概率标在图1中(用字母表示):
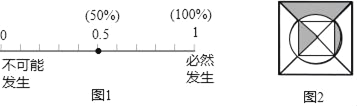
(1)记为点A:随意掷两枚质地均匀的骰子,朝上面的点数之和为1;
(2)记为点B:抛出的篮球会下落;
(3)记为点C:从装有3个红球、7个白球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同);
(4)记为点D:如图2所示的正方形纸片上做随机扎针实验,则针头恰好扎在阴影区域内.
【答案】(1)0;(2)1;(3)![]() ;(4)
;(4)![]() .图中表示见解析.
.图中表示见解析.
【解析】
(1)先判断此事件为不可能事件,再根据不可能事件的概率为0求解;
(2)先判断此事件为必然事件,再根据必然事件的概率为1求解;
(3)先判断此事件为随机事件,再根据随机事件的概率公式求出概率值;
(4)先判断此事件为随机事件,再根据随机事件的概率公式求出概率值.然后依次标在图中即可.
(1)随意掷两枚质地均匀的骰子,朝上面的点数之和为1为不可能事件,其概率为0;
(2)为必然事件,其概率为1;
(3)从装有3个红球、7个白球的口袋中任取一个球,恰好是白球,是随机事件,其概率为![]() ;
;
(4)如图2所示的正方形纸片上做随机扎针实验,则针头恰好扎在阴影区域内的概率为![]() ;
;
如图所示:


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
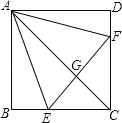
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有____.(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
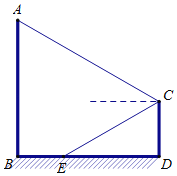
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底和,并且等于两底和的一半.
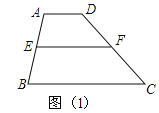
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF=![]() (AD+BC)
(AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点
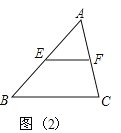
请你运用所学知识,结合上述材料,解答下列问题.
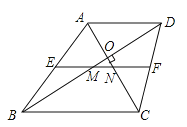
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD=![]() ,OC=5,求MN的长.
,OC=5,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
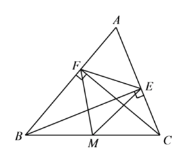
【题目】如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.
(1) 求证:△MEF是等腰三角形;
(2) 若∠A=![]() ,∠ABC=50°,求∠EMF的度数.
,∠ABC=50°,求∠EMF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.

(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,连接DF,且P是线段DF的中点,连接PG,PC.
(1)如图1中,PG与PC的位置关系是 ,数量关系是 ;
(2)如图2将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变,求证:PG=PC;
(3)如图3,若将条件“正方形ABCD和正方形BEFG”改为“菱形ABCD和菱形BEFG”,点A,B,E在同一条直线上,连接DF,P是线段DF的中点,连接PG、PC,且∠ABC=∠BEF=60°,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com