
【题目】如图1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,连接DF,且P是线段DF的中点,连接PG,PC.
(1)如图1中,PG与PC的位置关系是 ,数量关系是 ;
(2)如图2将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变,求证:PG=PC;
(3)如图3,若将条件“正方形ABCD和正方形BEFG”改为“菱形ABCD和菱形BEFG”,点A,B,E在同一条直线上,连接DF,P是线段DF的中点,连接PG、PC,且∠ABC=∠BEF=60°,求![]() 的值.
的值.

【答案】(1)PG⊥PC且PG=PC;(2)详见解析;(3)PG:PC=![]() .
.
【解析】
(1)延长GP交DC于点H,由条件可以得出△DHP≌△FGP,就可以得出DH=GF,PH=PG,根据正方形的性质就可以得出HC=GC,从而由等腰直角三角形的性质可以得出结论;
(2)如图2,延长GP交DC于点H,由条件可以得出△DHP≌△FGP,根据直角三角形的性质就可以得出结论;
(3)如图2,延长GP交DC于点H,由条件可以得出△DHP≌△FGP,根据菱形的性质可以得出△HCG是等腰三角形,由菱形的内角和可以求出∠PCG=60°,由特殊角的三角函数值就可以求出结论.
(1)PG⊥PC且PG=PC.理由:
如图1,延长GP交DC于点H.
∵四边形ABCD和BEFG是正方形,∴DC=BC,BG=GF,∠FGB=∠GCD=∠DCB=90°,∴CD∥GF,∴∠CDP=∠GFP.
∵P是线段DF的中点,∴DP=FP.
在△DHP和△FGP中,∵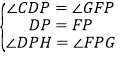 ,∴△DHP≌△FGP(ASA),∴DH=FG,PH=PG,∴HC=GC,∴△HCG是等腰直角三角形.
,∴△DHP≌△FGP(ASA),∴DH=FG,PH=PG,∴HC=GC,∴△HCG是等腰直角三角形.
∵PH=PG,∴PG⊥PC且PG=PC.
(2)如图2,延长GP交DC于点H.
∵四边形ABCD和BEFG是矩形,∴∠FGB=∠GCD=∠DCB=90°,∴CD∥GF,∴∠CDP=∠GFP.
∵P是线段DF的中点,∴DP=FP.
在△DHP和△FGP中,∵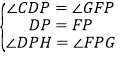 ,∴△DHP≌△FGP(ASA),∴PH=PG=
,∴△DHP≌△FGP(ASA),∴PH=PG=![]() HG.
HG.
∵∠DCB=90°,∴△HCG是直角三角形,∴CP=![]() HG,∴PG=PC;
HG,∴PG=PC;
(3)如图3,延长GP交CD于H.
∵P是DF的中点,∴DP=FP.
∵四边形ABCD和四边形BEFG是菱形,点A,B,E在同一条直线上,∴DC∥GF,∴∠HDP=∠GFP.
在△DHP和△FGP中,∵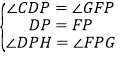 ,∴△DHP≌△FGP(ASA),∴HP=GP,DH=FG.
,∴△DHP≌△FGP(ASA),∴HP=GP,DH=FG.
∵CD=CB,FG=GB,∴CD﹣DH=CB﹣FG,即:CH=CG,∴△HCG是等腰三角形,∴PC⊥PG,∠HCP=∠GCP(等腰三角形三线合一),∴∠CPG=90°.
∵∠ABC=60°,∴∠DCB=120°,∴∠GCP=![]() ∠DCB=60°,∴Rt△CPG中,
∠DCB=60°,∴Rt△CPG中,![]() .
.
故答案为:PG⊥PC,PG=PC,PG:PC=![]() .
.


科目:初中数学 来源: 题型:
【题目】请将下列事件发生的概率标在图1中(用字母表示):
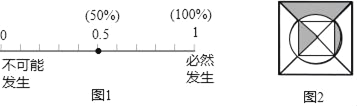
(1)记为点A:随意掷两枚质地均匀的骰子,朝上面的点数之和为1;
(2)记为点B:抛出的篮球会下落;
(3)记为点C:从装有3个红球、7个白球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同);
(4)记为点D:如图2所示的正方形纸片上做随机扎针实验,则针头恰好扎在阴影区域内.
查看答案和解析>>
科目:初中数学 来源: 题型:
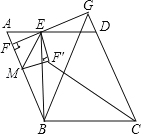
【题目】如图,平行四边形ABCD中,过点B作BE⊥AD于点E,过点E作EF⊥AB于点F,与CD的延长线交于点G,连接BG,且BE=BC,BG=5![]() ,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m-3)x+m+1经过点A(1,4)
(1)求m的值;
(2)画出此一次函数的图象;
(3)若一次函数交y轴于点B,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线![]() 经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k值是( )
经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k值是( )
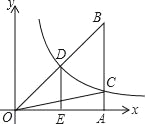
A. 3 B. 2 C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
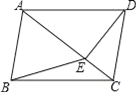
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com