
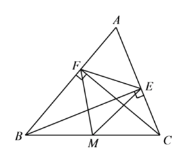
【题目】如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.
(1) 求证:△MEF是等腰三角形;
(2) 若∠A=![]() ,∠ABC=50°,求∠EMF的度数.
,∠ABC=50°,求∠EMF的度数.
【答案】(1)见解析;(2)∠EMF=40°
【解析】
(1)易得△BCE和△BCF都是直角三角形,根据直角三角形斜边上的中线等于斜边的一半可得ME=MF=![]() BC,即可得证;
BC,即可得证;
(2)首先根据三角形内角和定理求出∠ACB=60°,然后由(1)可知MF=MB,ME=MC,利用等边对等角可求出∠MFB=50°,∠MEC=60°,从而推出∠BMF和∠CME的度数,即可求∠EMF的度数.
(1)∵CF⊥AB于点F,BE⊥AC于点E,
∴△BCE和△BCF为直角三角形
∵M为BC的中点
∴ME=![]() BC,MF=
BC,MF=![]() BC
BC
∴ME=MF
即△MEF是等腰三角形
(2)∵∠A=70°,∠ABC=50°,
∴∠ACB=180°-70°-50°=60°
由(1)可知MF=MB,ME=MC,
∴∠MFB=∠ABC=50°,∠MEC=∠ACB=60°,
∴∠BMF=180°-2×50°=80°,∠CME=180°-2×60°=60°
∴∠EMF=180°-∠BMF-∠CME=180°-80°-60°=40°


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】(本题共10分)水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(1)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(2)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
(3)现需按毛利润的10%交纳各种税费,人工费每日按销售量每千克支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每千克涨价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
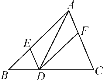
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
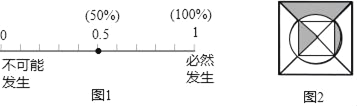
【题目】请将下列事件发生的概率标在图1中(用字母表示):
(1)记为点A:随意掷两枚质地均匀的骰子,朝上面的点数之和为1;
(2)记为点B:抛出的篮球会下落;
(3)记为点C:从装有3个红球、7个白球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同);
(4)记为点D:如图2所示的正方形纸片上做随机扎针实验,则针头恰好扎在阴影区域内.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,AC是ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
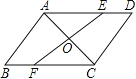
(1)求证:△AOE≌△COF;
(2)当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
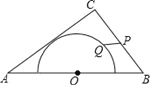
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
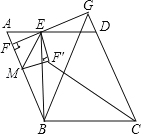
【题目】如图,平行四边形ABCD中,过点B作BE⊥AD于点E,过点E作EF⊥AB于点F,与CD的延长线交于点G,连接BG,且BE=BC,BG=5![]() ,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com