
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
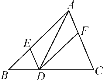
A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
【答案】C
【解析】
A选项,∵在△ABC中,点D在BC上,DE∥AC,DF∥AB,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形;即A正确;
B选项,∵四边形AEDF是平行四边形,∠BAC=90°,
∴四边形AEDF是矩形;即B正确;
C选项,因为添加条件“AD平分∠BAC”结合四边形AEDF是平行四边形只能证明四边形AEDF是菱形,而不能证明四边形AEDF是矩形;所以C错误;
D选项,因为由添加的条件“AB=AC,AD⊥BC”可证明AD平分∠BAC,从而可通过证∠EAD=∠CAD=∠EDA证得AE=DE,结合四边形AEDF是平行四边形即可得到四边形AEDF是菱形,所以D正确.
故选C.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
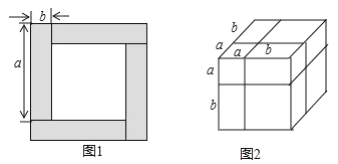
【题目】通常情况下,用两种不同的方法计算同一图形的面积,可以得到一个恒等式,
①如图1,根据图中阴影部分的面积可表示为__________,还可表示为___________,可以得到的恒等式是___________.
②类似地,用两种不同的方法计算同一各几何体的体积,也可以得到一个恒等式,如图2是边长为![]() 的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为 40m 的栅栏围住(如图).设绿化带的BC 边长为x m,绿化带的面积为y m2 . 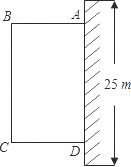
(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围.
(2)当x 为何值时,满足条件的绿化带的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
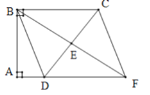
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() ,
,![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求![]() 、
、![]() 的长;
的长;
(2)求证:![]() ;
;
(3)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信支付、转账,把微信账户里的钱转到银行卡叫做提现,自2016年3月1日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为1800元,他需支付手续费_____元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下,问:小明3次提现金额共计多少元?
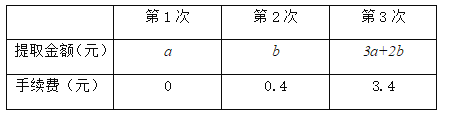
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).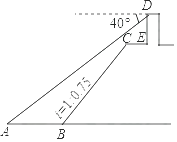
A.5.1米
B.6.3米
C.7.1米
D.9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,E 为 BC 的中点,F 是 CD 上一点,且 CF ![]() CD ,
CD ,

求证:(1)∠AEF=90°;
(2) ∠BAE=∠EAF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com