Question

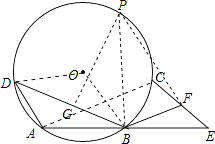
【题目】如图，已知⊙O上依次有A、B、C、D四个点， = ，连接AB、AD、BD，弦AB不经过圆心O，延长AB到E，使BE=AB，连接EC，F是EC的中点，连接BF．
（1）若⊙O的半径为3，∠DAB=120°，求劣弧 的长；
（2）求证：BF= BD；
（3）设G是BD的中点，探索：在⊙O上是否存在点P（不同于点B），使得PG=PF？并说明PB与AE的位置关系．

Answer 1

【答案】
（1）解：连接OB，OD，

∵∠DAB=120°，∴ 所对圆心角的度数为240°，

∴∠BOD=360°﹣240°=120°，

∵⊙O的半径为3，

∴劣弧 的长为： ×π×3=2π；

（2）证明：连接AC，

∵AB=BE，∴点B为AE的中点，

∵F是EC的中点，∴BF为△EAC的中位线，

∴BF= AC，

∵ = ，

∴ + = + ，

∴ = ，

∴BD=AC，

∴BF= BD；

（3）解：过点B作AE的垂线，与⊙O的交点即为所求的点P，

∵BF为△EAC的中位线，

∴BF∥AC，

∴∠FBE=∠CAE，

∵ = ，

∴∠CAB=∠DBA，

∵由作法可知BP⊥AE，

∴∠GBP=∠FBP，

∵G为BD的中点，

∴BG= BD，

∴BG=BF，

在△PBG和△PBF中，

，

∴△PBG≌△PBF（SAS），

∴PG=PF．

【解析】（1）利用圆心角定理进而得出∠BOD=120°，再利用弧长公式求出劣弧 的长；（2）利用三角形中位线定理得出BF= AC，再利用圆心角定理得出 = ，进而得出BF= BD；（3）首先过点B作AE的垂线，与⊙O的交点即为所求的点P，得出BP⊥AE，进而证明△PBG≌△PBF（SAS），求出PG=PF．