
如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
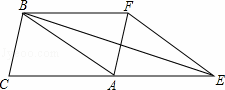
解:(1)由平移的性质得
AF∥BC,且AF=BC,△EFA≌△ABC
∴四边形AFBC为平行四边形
S△EFA=S△BAF=S△ABC=3
∴四边形EFBC的面积为9;
(2)BE⊥AF
证明:由(1)知四边形AFBC为平行四边形
∴BF∥AC,且BF=AC
又∵AE=CA
∴四边形EFBA为平行四边形又已知AB=AC
∴AB=AE
∴平行四边形EFBA为菱形
∴BE⊥AF;
(3)如上图,作BD⊥AC于D
∵∠BEC=15°,AE=AB
∴∠EBA=∠BEC=15°
∴∠BAC=2∠BEC=30°
∴在Rt△BAD中,AB=2BD
设BD=x,则AC=AB=2x
∵S△ABC=3,且S△ABC= AC•BD=
AC•BD= •2x•x=x2
•2x•x=x2
∴x2=3
∵x为正数
∴x=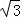
∴AC=2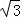 .
.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
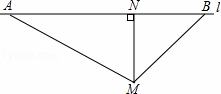
根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
(1)计算AB的长度.
(2)通过计算判断此车是否超速.
查看答案和解析>>
科目:初中数学 来源: 题型:
将点P(﹣2,3)向右平移3个单位得到点P1,点P2与点P1关于原点对称,则P2的坐标是( )
A. (﹣5,﹣3) B.(1,﹣3) C.(﹣1,﹣3) D. (5,﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com