
【题目】某新店开业宣传,进店有礼活动,店员们需准备制作圆柱体礼品纸盒(如图①),每个纸盒由1个长方形侧面和2个圆形底面组成,现有100张正方形纸板全部以A或者B方法截剪制作(如图②),设截剪时x张用A方法.

(1)根据题意,完成以下表格:
裁剪法A | 裁剪法B | |
长方形侧面 | x |
|
圆形底面 |
| 0 |
(2)若裁剪出的长方形侧面和圆形底面恰好用完,问能做多少个纸盒?
(3)按以上制作方法,若店员们希望准备300个礼盒,那至少还需要正方形纸板 张.
【答案】(1)2(100﹣x),8x;(2)160个;(3)88
【解析】
(1)由题意得出截剪时(100﹣x)张用B方法,一共能截剪出2(100﹣x)个长方形侧面,没有圆形底面,由每张正方形纸板用A方法截剪出8个圆形和1个长方形,得出一共能截剪出8x个圆形和x个长方形,即可得出结果;
(2)由题意得x+2(100﹣x)=![]() ×8x,解得x=40,则
×8x,解得x=40,则![]() ×8×40=160;
×8×40=160;
(3)由题意得需要300×2÷8=75(张)纸板截剪圆形底面,需要(300﹣75)÷2=112.5≈113(张)纸板截剪长方形侧面,共用正方形纸板75+113=188(张),则至少还需要正方形纸板188﹣100=88(张).
解:(1)∵设截剪时x张用A方法,
∴截剪时(100﹣x)张用B方法,
∵每张正方形纸板用B方法,只能截剪2个长方形,
∴一共能截剪出2(100﹣x)个长方形侧面,没有圆形底面,
∵每张正方形纸板用A方法截剪出8个圆形和1个长方形,
∴一共能截剪出8x个圆形和x个长方形,
故答案为:2(100﹣x),8x;
(2)若裁剪出的长方形侧面和圆形底面恰好用完,
由题意得:x+2(100﹣x)=![]() ×8x,
×8x,
解得:x=40,
∴![]() ×8×40=160(个);
×8×40=160(个);
答:若裁剪出的长方形侧面和圆形底面恰好用完,能做160个纸盒;
(3)由题意得:需要300×2÷8=75(张)纸板截剪圆形底面,需要(300﹣75)÷2=112.5≈113(张)纸板截剪长方形侧面,
∴共用正方形纸板:75+113=188(张),
∴至少还需要正方形纸板:188﹣100=88(张),
故答案为:88.


科目:初中数学 来源: 题型:
【题目】纪中三鑫双语学校准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种).

根据以上统计图提供的信息,请解答下列问题:
(1)m= ,n= .
(2)补全上图中的条形统计图.
(3)在抽查的m名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B坐标分别为A(0,a)、B(b,a),且a,b满足:(a-3)2+![]() =0,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.
=0,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.

(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在点M,连接MC、MD,使S△MCD=四边形ABDC?若存在这样的点,求出点M的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA、PO,当点P在BD上移动时(不与B、D重合),![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
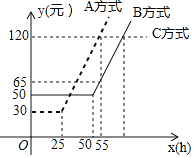
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 、
、![]() 三点在同一条直线上,
三点在同一条直线上,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
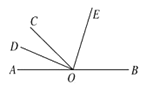
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() ;
;
(3)![]() 是否随
是否随![]() 的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,小慧同学利用直尺和规进行了如下操作:①连接AC,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
(1)线段AF与CF的数量关系是 .
(2)若∠BAD=120°,AE平分∠BAD,AB=8,求四边形AECF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=OB=8,OD=1,点C为线段AB的中点
(1)直接写出点C的坐标 ;
(2)求直线CD的解析式;
(3)在平面内是否存在点F,使得以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com