
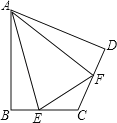
【题目】在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点.
(1)若∠ABC=∠ADC,∠BAE=30°,AD=3,求AE的长;
(2)若∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据已知条件得到∠ABC=∠ADC=90°,根据直角三角形的性质即可得到结论;
(2)延长CB到G,使BG=DF,证明△ABG≌△ADF,根据全等三角形的性质得到AG=AF,∠GAB=∠FAD,证明△AEG≌△AEF,根据全等三角形的性质证明.
(1)解:∵AB=AD,AD=3,
∴AB=3,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∵∠BAE=30°,
∴AE=![]() AB=
AB=![]() ;
;
(2)证明:延长CB到G,使BG=DF,
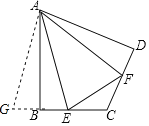
∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,
∴∠ADC=∠ABG,
在△ABG和△ADF中,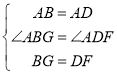 ,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠FAD,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠FAD+∠BAE=∠GAB+∠BAE=![]() ∠BAD,
∠BAD,
∴∠GAE=∠FAE,
在△AEG和△AEF中,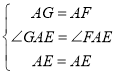 ,
,
∴△AEG≌△AEF(SAS),
∴EF=GE,
∴EF=BE+BG=BE+DF.


科目:初中数学 来源: 题型:
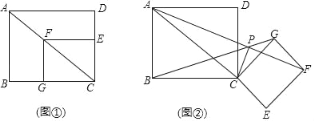
【题目】如图①,四边形ABCD与四边形CEFG都是矩形,点E,G分别在边CD,CB上,点F在AC上,AB=3,BC=4
(1)求![]() 的值;
的值;
(2)把矩形CEFG绕点C顺时针旋转到图②的位置,P为AF,BG的交点,连接CP
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断CP与AF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
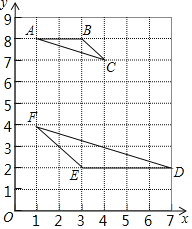
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.
查看答案和解析>>
科目:初中数学 来源: 题型:
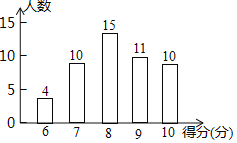
【题目】为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)直接写出本次调查获取的样本数据的平均数为 ,中位数为 ;
(3)社区决定对该小区1500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州区初中数学教研工作坊到重庆某中学开展研讨活动,先后乘坐甲、乙两辆汽车从万州出发前往相距250千米的重庆,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到重庆,如图是甲、乙两车之间的距离s(km),乙车出发时间t(h)之间的函数关系图象,则甲车从万州出发到重庆共花费了_____小时.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
(1)求抛物线表达式;
(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;
(3)当△PBQ为等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
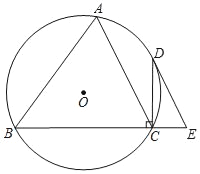
【题目】如图,△ABC内接于⊙O,过点C作BC的垂线交⊙O于D,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
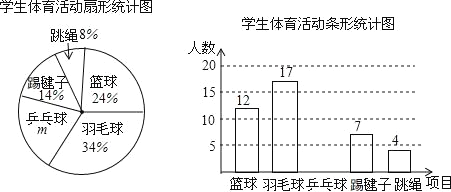
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com