
����Ŀ��Ϊ���˽�ȫУ1500��ѧ����ѧУ���õ�������ë��ƹ��������ӡ�������5���������ϲ���������ȫУ��Χ�������鲿��ѧ����������ϲ����������Ŀ��ÿ��ֻѡһ��������ʾ����飬��ͳ�����ݻ��Ƴ���ͼ����������ͳ��ͼ�������ͼ���ṩ����Ϣ������и��⣮
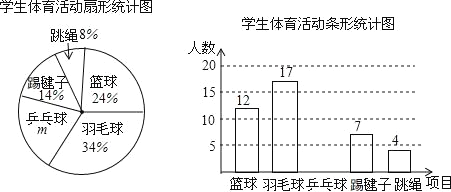
��1��m= %����ι���ȡ�� ��ѧ�����е��飻����ȫ����ͼ��
��2��������Ƹ�УԼ�� ��ѧ��ϲ��������
��3����ѧУ����ϲ���������4�ˣ�����һŮ�������ѡȡ2�˽������ܲ��ԣ��������б�����״ͼ�ķ�������鵽һ��һŮѧ���ĸ����Ƕ��٣�
���𰸡���1��20��50����2��360����3��![]() .
.
��������
�����������1������������ͼ������ͼ�����m=100%-14%-8%-24%-34%=20%����������������4�ˣ�ռ�İٷֱ�Ϊ8%���ɵ�������4��8%=50��
��2����1500��24%=360��������ø�УԼ��360��ѧ��ϲ��������
��3�����ȸ������⻭������Ȼ���ɱ���������еȿ��ܵĽ����鵽һ��һŮѧ��������������ø��ʹ�ʽ������ô𰸣�
�����������1��m=100%-14%-8%-24%-34%=20%��
��������������4�ˣ�ռ�İٷֱ�Ϊ8%��
��4��8%=50��
��ͼ��ʾ��50��20%=10���ˣ���
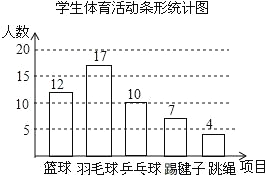
��2��1500��24%=360��
��3���б����£�
��1 | ��2 | ��3 | ٠| |
��1 | ��2����1 | ��3����1 | ����1 | |
��2 | ��1����2 | ��3����2 | ����2 | |
��3 | ��1����3 | ��2����3 | ����3 | |
٠| ��1��٠| ��2��٠| ��3��٠|
�����п��ܳ��ֵĽ����12�����������ÿ��������ֵĿ�������ȣ�����һ��һŮ�������6�֣�
��鵽һ��һŮ�ĸ���P=![]() .
.


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
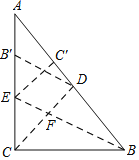
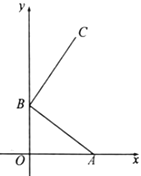
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬BC��3��AC��4����CD�۵���ʹ��B����CA���ϵ�B�䴦��չ��������BE�۵���ʹ��C����BA���ϵ�C�䴦��CD��BE���ڵ�F��
��1����AC��ij��ȣ�
��2����CE�ij��ȣ�
��3���Ƚ��ı���EC��DF���BCF����Ĵ�С����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
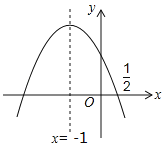
����Ŀ����4�֣���ͼ��������![]() �ĶԳ�����
�ĶԳ�����![]() ���ҹ��㣨
���ҹ��㣨![]() ��0���������н��ۣ���abc��0����a��2b+4c=0����25a��10b+4c=0����3b+2c��0����a��b��m��am��b��������������ȷ�Ľ����� ������д��ȷ���۵���ţ�
��0���������н��ۣ���abc��0����a��2b+4c=0����25a��10b+4c=0����3b+2c��0����a��b��m��am��b��������������ȷ�Ľ����� ������д��ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ��������һ����ˮ����ʵ�����DZ߳�Ϊm��������ȥ��һ���߳�Ϊn�ף�m��n����������ˮ�غ����µIJ��֣������˶�����ˮ�����������DZ߳�Ϊ��m-n���������Σ������������ˮ�����ջ���aǧ�ˣ�
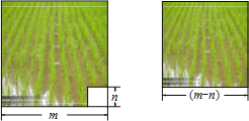
��1������ˮ���ĵ�λ��������ߣ�Ϊʲô��
��2���ߵĵ�λ��������ȵ͵ĵ�λ��������߶��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABC�������������ֱ�ΪA��0����3����B��3����2����C��2����4���������������У�ÿ��С�����εı߳���1����λ���ȣ�
��1��������ABC����ƽ��6����λ�õ�����A1B1C1��
��2���Ե�CΪλ�����ģ��������л�����A2B2C2��ʹ��A2B2C2����ABCλ�ƣ�����A2B2C2����ABC��λ�Ʊ�Ϊ2��1����ֱ��д����A2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b�뷴��������![]() ��ͼ����A(2��4)��B(-4��n)���㣬��x���ڵ�C��
��ͼ����A(2��4)��B(-4��n)���㣬��x���ڵ�C��

(1)��m��n��ֵ��
(2)��ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
(3)��x���·���ͼ����x�ᷭ�ۣ���B���ڵ�B����������AB�䡢B��C������A B��C�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
С����ѧϰ���θ�ʽ�Ļ��������������һ����Ҫ�����ʽ�ӣ�![]() ������λ����أ�˼����������3+2
������λ����أ�˼����������3+2![]() =1+2
=1+2![]() +��
+��![]() ��2=��1+
��2=��1+![]() ��2������
��2������![]() =
=![]() =1+
=1+![]() ������˼����С����������̽������a+b
������˼����С����������̽������a+b![]() =��m+n
=��m+n![]() ��2ʱ������a��b��m��n��Ϊ������������a+b
��2ʱ������a��b��m��n��Ϊ������������a+b![]() =m2+2
=m2+2![]() mn+2n2����ʱ��a=m2+2n2��b=2mn�����ǣ�
mn+2n2����ʱ��a=m2+2n2��b=2mn�����ǣ�![]() =m+n
=m+n![]() ���������С���ķ���̽��������������⣺
���������С���ķ���̽��������������⣺
��1����a��b��m��n����������![]() =m+n
=m+n![]() ���ú�m��n��ʽ�ӷֱ��ʾa��bʱ�������a=�� ����b=�� ����
���ú�m��n��ʽ�ӷֱ��ʾa��bʱ�������a=�� ����b=�� ����
��2�����ã�1���еĽ��ۣ�ѡ��һ����������գ�![]() =�� ��+�� ��
=�� ��+�� ��![]() ��
��
��3������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ��������
��������![]() ����
����![]() ��������
��������![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת90���õ��߶�
��ʱ����ת90���õ��߶�![]() �����
�����![]() �������ǣ� ��
�������ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+3�ĶԳ�����ֱ��x=1��
��1����֤��2a+b=0��
��2��������x�ķ���ax2+bx��8=0��һ����Ϊ4���̵���һ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com