
【题目】关于反比例函数y=﹣ ![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.图像在第一、三象限
B.图像经过(2,1)
C.在每个象限中,y随x的增大而减小
D.当x>1时,﹣2<y<0
【答案】D
【解析】解:A、反比例函数y=﹣ ![]() 中的﹣2<0,则该函数图像经过第二、四象限,故本选项错误; B、反比例函数y=﹣
中的﹣2<0,则该函数图像经过第二、四象限,故本选项错误; B、反比例函数y=﹣ ![]() 中的﹣2<0,则该函数图像经过第二、四象限,、而点(2,1)位于第一象限,即该函数图像不经过(2,1),故本选项错误;
中的﹣2<0,则该函数图像经过第二、四象限,、而点(2,1)位于第一象限,即该函数图像不经过(2,1),故本选项错误;
C、反比例函数y=﹣ ![]() 中的﹣2<0,在每个象限内,y随x的增大而增大,故本选项错误;
中的﹣2<0,在每个象限内,y随x的增大而增大,故本选项错误;
D、反比例函数y=﹣ ![]() 中的﹣2<0,在每个象限内,y随x的增大而增大,所以当x>1时,﹣2<y<0,故本选项正确;
中的﹣2<0,在每个象限内,y随x的增大而增大,所以当x>1时,﹣2<y<0,故本选项正确;
故选:D.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE, 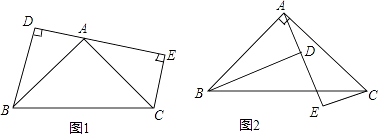
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
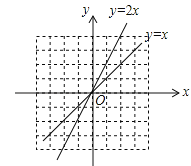
【题目】如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的![]() 倍,纵坐标不变,得到函数y=2x的图象.
倍,纵坐标不变,得到函数y=2x的图象.
类似地,我们可以认识其他函数.
(1)把函数![]() 的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数
的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数![]() 的图象;也可以把函数
的图象;也可以把函数![]() 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数
的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数![]() 的图象.
的图象.
(2)已知下列变化:①向下平移2个单位长度;②向右平移1个单位长度;③向右平移![]() 个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的
个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的![]() 倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
(Ⅰ)函数![]() 的图象上所有的点经过④→②→①,得到函数 的图象;
的图象上所有的点经过④→②→①,得到函数 的图象;
(Ⅱ)为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象上所有的点 .
的图象上所有的点 .
A.①→⑤→③B.①→⑥→③C.①→②→⑥D.①→③→⑥
(3)函数![]() 的图象可以经过怎样的变化得到函数
的图象可以经过怎样的变化得到函数![]() 的图象?(写出一种即可)
的图象?(写出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子产品经过11月、12月连续两次降价,售价由3900元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )
A. 3900(1+x)2=2500 B. 3900(1﹣x)2=2500
C. 3900(1﹣2x)=2500 D. 2500(1+x)2=3900
查看答案和解析>>
科目:初中数学 来源: 题型:
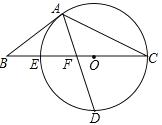
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:探索发现
(1)分解因式:①(1+x)+x(1+x)=()()=()2
②(1+x)+x(1+x) + x(1+x)2=
③(1+x)+x(1+x) + x(1+x)2 + x(1+x)3=
(2)根据(1)的规律,直接写出多项式:(1+x) +x(1+x) + x(1+x)2+…+ x(1+x)2017分解因式的结果:。
(3)变式: ![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+2x=4,配方结果正确的是( )
A. (x+1)2=4 B. (x+2)2=4 C. (x+2)2=5 D. (x+1)2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1.2计算3.4分解因式)
(1)( ![]() +1)0﹣(﹣
+1)0﹣(﹣ ![]() )2+2﹣2
)2+2﹣2
(2)(2a﹣3b)(﹣3b﹣2a)
(3)3m2﹣24m+48
(4)x3y﹣4xy.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com