Question

【题目】如图所示，平行四边形ABCD和平行四边形CDEF有公共边CD，边AB和EF在同一条直线上，AC⊥CD且AC=AF，过点A作AH⊥BC交CF于点G，交BC于点H，连接EG．

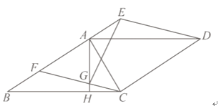
（1）若AE=2，CD=5，则△BCF的面积为 ；△BCF的周长为 ；

（2）求证：BC=AG+EG．

Answer 1

【答案】（1）3，；（2）见解析

【解析】

（1）根据平行和垂直的特点求出BF，AF，再根据勾股定理求出CD，根据FP与BA的比值求出面积，再根据勾股定理求CF，BC即可得到周长．

（2）在AD上截取AM=AG，连接CM，证△FAG≌△CAM；证△EFG≌△DCM．

解：（1）面积为3；周长为

∵四边形ABCD和四边形CDEF都是平行四边形，

∴EF=CD，AB=CD，AB∥CD

∴EF=AB=CD=5

∴AE=EF-AE=5-2=3

∴BF=5-3=2

过F作FP⊥BC

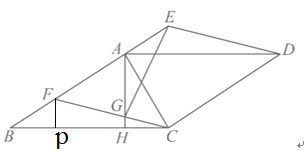
则FP：AH=BF：AB=2：5，

∴ ,

∵AC⊥CD，AB∥CD,

∴AB⊥AC，即∠BAC=90°，

∵AC=AF=3,

∴CF= ，BC= ，

∴

∴△BCF的面积为3，△BCF周长为

（2）在AD上截取AM=AG，连接CM，

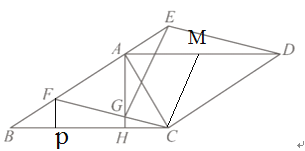
∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC

∵AH⊥BC

∴AD⊥AH

∴∠DAH=90°

∵∠BAC=90°

∴∠DAH=∠BAC

∴∠DAH-∠CAH =∠BAC-∠CAH

∴∠BAH=∠CAD

∵AF=AC

∴△FAG≌△CAM

∴FG=CM，∠ACM=∠AFG

∵四边形CDEF是平行四边形，

∴EF∥CD，EF=CD，

∴∠DCF+∠AFC=180°，

∵AF=AC， ∠BAC=90°，

∴∠AFC=∠ACF=45°，

∴∠DCF=180°-∠AFC=135°，

∴∠ACM=∠AFG=45°，

∴∠DCM=∠FCD-∠ACF-∠ACM=45°，

∴∠AFG=∠DCM，

∴△EFG≌△DCM，

∴EG=DM，

∵AD=AM+DM，

∴AD=AG+EG，

∵AD=BC，

∴BC=AG+EG．