
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E, DF∥AB交BC于点F .
(1)求证:四边形BEDF是菱形
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.

【答案】(1)见详解;(2)35°
【解析】
(1)由题意可证BE=DE,四边形BEDF是平行四边形,即可证四边形BEDF为菱形;
(2)由三角形内角和定理求出∠ABC=70°,由菱形的性质即可得出答案.
(1)证明:∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF=![]() ∠ABC
∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=80°,∠C=30°,
∴∠ABC=180°-80°-30°=70°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=70°,∠BDE=![]() ∠EDF=35°.
∠EDF=35°.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是( )
A. 57.5° B. 32.5° C. 57.5°,23.5° D. 57.5°,32.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
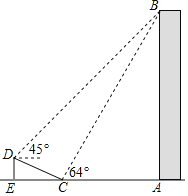
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.
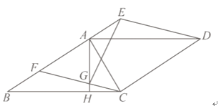
(1)若AE=2,CD=5,则△BCF的面积为 ;△BCF的周长为 ;
(2)求证:BC=AG+EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A在原点O的左边,表示的数为﹣10,点B在原点的右边,且BO=3AO.点M以每秒3个单位长度的速度从点A出发向右运动.点N以每秒2个单位长度的速度从点O出发向右运动(点M,点N同时出发).
(1)数轴上点B对应的数是 ,点B到点A的距离是 ;
(2)经过几秒,原点O是线段MN的中点?
(3)经过几秒,点M,N分别到点B的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
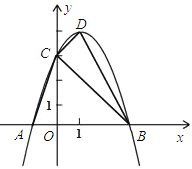
【题目】如图,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0)和B,与y轴交于点C(0,3).
(1)求此抛物线的解析式及点B的坐标;
(2)设抛物线的顶点为D,连接CD、DB、CB、AC.
①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com