
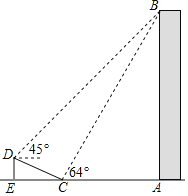
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
【答案】(1)斜坡CD的高度DE是5米;(2)大楼AB的高度是34米.
【解析】试题分析:(1)根据在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1: ![]() ,高为DE,可以求得DE的高度;
,高为DE,可以求得DE的高度;
(2)根据锐角三角函数和题目中的数据可以求得大楼AB的高度.
试题解析:(1)∵在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1: ![]() ,
,
∴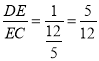 ,
,
设DE=5x米,则EC=12x米,
∴(5x)2+(12x)2=132,
解得:x=1,
∴5x=5,12x=12,
即DE=5米,EC=12米,
故斜坡CD的高度DE是5米;
(2)过点D作AB的垂线,垂足为H,设DH的长为x,
由题意可知∠BDH=45°,
∴BH=DH=x,DE=5,
在直角三角形CDE中,根据勾股定理可求CE=12,AB=x+5,AC=x-12,
∵tan64°=![]() ,
,
∴2=![]() ,
,
解得,x=29,AB=x+5=34,
即大楼AB的高度是34米.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF

(1)求∠CDE的度数
(2)求证:DF是⊙O的切线
查看答案和解析>>
科目:初中数学 来源: 题型:
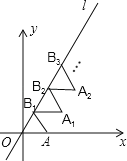
【题目】如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东同学根据函数的学习经验,对函数y ![]()
![]() 进行了探究,下面是他的探究过程:
进行了探究,下面是他的探究过程:
(1)已知x=-3时![]() 0;x=1 时
0;x=1 时![]() 0,化简:
0,化简:
①当x<-3时,y= ;
②当-3≤x≤1时,y= ;
③当x>1时,y= .
(2)在平面直角坐标系中画出y=|x﹣1|+|x+3|的图象,根据图象,写出该函数的一条性质: ;

查看答案和解析>>
科目:初中数学 来源: 题型:
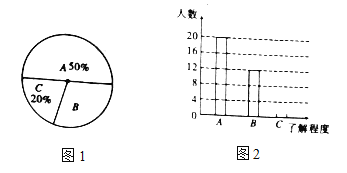
【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E, DF∥AB交BC于点F .
(1)求证:四边形BEDF是菱形
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() 第三次点
第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com