
分析 (1)根据①②步骤列出代数式,做差后即可得出结论;
(2)结合(1)可知3a+3=120,解之即可得出结论;
(3)根据最后结果为3a+3,写出求a的过程即可.
解答 解:(1)由题意可知,第①步运算的结果为:2(2a+9)=4a+18;
第②步运算的结果为:$\frac{1}{2}$(2a+30)=a+15;
第③步运算的为:(4a+18)-(a+15)=3a+3.
(2)∵最后结果为120,
∴3a+3=120,
解得:a=39.
答:小明最初想的两位数是39.
(3)陈老师猜数的方法是:将学生所得的最后结果减去3,再除以3.
点评 本题考查了一元一次方程的应用以及列代数,根据数量关系列出代数式(或一元一次方程)是解题的关键.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:填空题
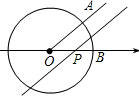 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是0<x≤$\sqrt{2}$.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是0<x≤$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
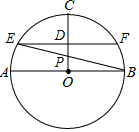 如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.
如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
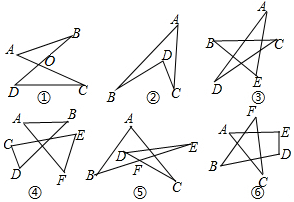
 如图,将45°角三角板绕直角顶点旋转.
如图,将45°角三角板绕直角顶点旋转.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com