

分析 (1)根据角的平分线的定义以及三角形的外角的性质即可求解;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC和∠BCE,再根据角平分线的定义求出∠OBC+∠OCB,然后根据三角形内角和定理列式整理即可得解;
(3)根据四边形内角和等于360°求出∠ABC+∠BCD,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形内角和定理列式整理即可得解.
解答 解:(1)探究2结论:∠BOC=$\frac{1}{2}$∠A.
理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCD=$\frac{1}{2}$∠ACD,
又∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠ABC,
∴∠OCD=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠A+∠OBC,
又∵∠OCD是△BOC的一个外角,
∴∠BOC=∠OCD-∠OBC=$\frac{1}{2}$∠A+∠OBC-∠OBC=$\frac{1}{2}$∠A;
(2)探究3:结论∠BOC=90°-$\frac{1}{2}$∠A.
理由是:∵BO平分∠BDC,CO平分∠ECB,
∴∠BOC=$\frac{1}{2}$∠DBC,∠OCB=$\frac{1}{2}$∠ECB,
又∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠BOC+∠OCB=$\frac{1}{2}$(∠A+∠ABC+∠ACB+∠A)=$\frac{1}{2}$(180°+∠A),
又∵∠BOC=180°-(∠BOC+∠OCB)=180°-$\frac{1}{2}$(180°+∠A)=90°-$\frac{1}{2}$∠A;
(3)拓展:结论∠BOC=$\frac{1}{2}$(∠A+∠D).
理由是:∵BO平分∠ABC,CO平分∠DCB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠DCB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠DCB),
又∵∠ABC+∠DCB+∠A+∠D=360°,即∠ABC+∠DCB=360°-∠A-∠D,
∴∠OBC+∠OCB=$\frac{1}{2}$(360°-∠A+∠D),
∴∠BOC=180°-(∠OBC+∠OCB)=$\frac{1}{2}$(∠A+∠D).
点评 本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 70cm | B. | 105cm | C. | 230cm | D. | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
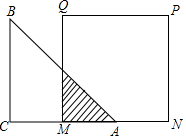 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合.
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x1-x2)(x1+x2+2)>0 | B. | (x1-x2)(x1+x2+2)<0 | ||
| C. | -a(x1-x2)(x1+x2+2)>0 | D. | a(x1-x2)(x1+x2+2)<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com