
分析 (1)设y=kx+b,根据题意,利用待定系数法确定出y与x的函数关系式即可;
(2)根据题意结合销量×每本的利润=150,进而求出答案;
(3)根据题意结合销量×每本的利润=w,进而利用二次函数增减性求出答案.
解答 解:(1)设y=kx+b,
把(22,36)与(24,32)代入得:$\left\{\begin{array}{l}{22k+b=36}\\{24k+b=32}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=80}\end{array}\right.$,
则y=-2x+80;
(2)设当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是x元,
根据题意得:(x-20)y=150,
则(x-20)(-2x+80)=150,
整理得:x2-60x+875=0,
(x-25)(x-35)=0,
解得:x1=25,x2=35,
∵20≤x≤28,
∴x=35(不合题意舍去),
答:每本纪念册的销售单价是25元;
(3)由题意可得:
w=(x-20)(-2x+80)
=-2x2+120x-1600
=-2(x-30)2+200,
此时当x=30时,w最大,
又∵售价不低于20元且不高于28元,
∴x<30时,y随x的增大而增大,即当x=28时,w最大=-2(28-30)2+200=192(元),
答:该纪念册销售单价定为28元时,才能使文具店销售该纪念册所获利润最大,最大利润是192元.
点评 此题主要考查了二次函数的应用以及一元二次方程的应用、待定系数法求一次函数解析式等知识,正确利用销量×每本的利润=w得出函数关系式是解题关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | m |
| C | 1<t≤1.5 | n |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
 ①
①查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a(a-b)=-a2-ab | B. | (2ab)2÷a2b=4ab | C. | 2ab•3a=6a2b | D. | (a-1)(1-a)=a2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x2y2(2x-1) | B. | 3xy(2x-1) | C. | xy2(2x-1) | D. | xy(2x-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
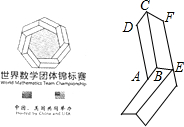 第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )| A. | 7(a+b+c-d) | B. | 7(a+b-c+d) | C. | 7(a-b+c+d) | D. | 7(b+c+d-a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com