
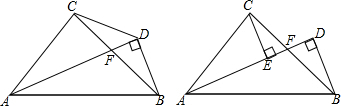
分析 (1)根据∠ACB=∠ADB=90°,得出A,B,C,D四点共圆,根据圆周角定理和等腰三角形的判定即可得到结论;
(2)延长AC,BD交于点M,得到△ADM≌△ABD,作出BD=DM,AM=AB,由(1)证得A,B,C,D四点共圆,由圆周角定理推出CD=BD,由于CE∥BM,于是得到$\frac{CE}{DM}=\frac{AC}{AM}=\frac{AC}{AB}=\frac{1}{\sqrt{2}}$,求出∠ECD=∠ECF+∠FCD=∠DAB+∠DAC=45°于是得到结论;
(3)由于△AFC≌△BCM,得到AF=BM=2BD,推出△ADB∽BDF,得到$\frac{DF}{BD}=\frac{BD}{AD}$,通过化简得到$\frac{2DF}{AF}+2-\frac{AF}{DF}$=0,设$\frac{DF}{AF}$=x,解方程2x+2-$\frac{1}{x}$=0,即可得到结果.
解答 解:(1)∵∠ACB=∠ADB=90°,
∴A,B,C,D四点共圆,
∴∠DCB=∠DAB,∠DAC=∠DBC,
∴∠DCB=∠DBC,
∴BD=CD;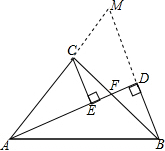
(2)延长AC,BD交于点M,
在△AMD与△ADB中,
$\left\{\begin{array}{l}{∠MAD=∠BAD}\\{AD=AD}\\{∠ADM=∠ADB}\end{array}\right.$,
∴△ADM≌△ABD,
∴BD=DM,AM=AB,
由(1)证得A,B,C,D四点共圆,
∵∠CAD=∠BAD,
∴$\widehat{CD}$=$\widehat{BD}$,
∴CD=BD,
∵CE⊥AD,
∴CE∥BM,
∴$\frac{CE}{DM}=\frac{AC}{AM}=\frac{AC}{AB}=\frac{1}{\sqrt{2}}$,
∴∠ECD=∠ECF+∠FCD=∠DAB+∠DAC=45°
∴DE=CE,∵DM=DB,∴$\frac{CE}{MD}=\frac{DE}{BD}=\frac{1}{\sqrt{2}}$,
∴BD=$\sqrt{2}$DE;
(3)在△AFC与△BCM中,
$\left\{\begin{array}{l}{∠CAF=∠CBM}\\{AC=BC}\\{∠ACF=∠BCM=90°}\end{array}\right.$,
∴△AFC≌△BCM,
∵∠DAB=∠DBF,∠ADB=∠BDF,
∴△ADB∽BDF,
∴$\frac{DF}{BD}=\frac{BD}{AD}$,即:$\frac{2DF}{2BD}=\frac{2BD}{DF+AD}$,
∴2DF(DF+AF)=AF2,
∴2DF2+2DF•AF=AF2=0,
∴$\frac{2DF}{AF}+2-\frac{AF}{DF}$=0,
设$\frac{DF}{AF}$=x,
∴2x+2-$\frac{1}{x}$=0,
解得:x=$\sqrt{3}$-1,
∴$\frac{DF}{AF}$=$\sqrt{3}$-1.
∴AF=BM=2BD,
∵∠DAB=∠DBF,∠ADB=∠BDF,
∴△ADB∽BDF,
∴$\frac{DF}{BD}=\frac{BD}{AD}$,即:$\frac{2DF}{2BD}=\frac{2BD}{DF+AD}$,
∴2DF(DF+AF)=AF2,
∴2DF2+2DF•AF=AF2=0,
∴$\frac{2DF}{AF}+2-\frac{AF}{DF}$=0,
设$\frac{DF}{AF}$=x,
∴2x+2-$\frac{1}{x}$=0,
解得:x=$\sqrt{3}$-1,
∴$\frac{DF}{AF}$=$\sqrt{3}$-1.
点评 本题考查了相似三角形的判定和性质.全等三角形的判定和性质,等腰直角三角形的性质,四点共圆,圆周角定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
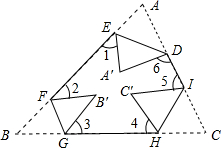 如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
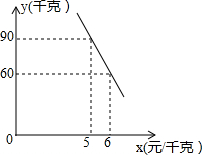 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.| 蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
| 所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
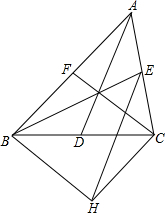 如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系.
如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$h≤z$<\frac{1}{3}$h | B. | $\frac{1}{3}$h≤z$<\frac{1}{2}$h | C. | $\frac{1}{2}$h≤z$<\frac{3}{4}$h | D. | $\frac{3}{4}h≤z<h$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com