
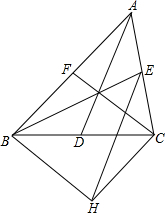
 如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系.
如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系. 分析 AD∥EH,连结FH交BC于D',利用已知条件和平行四边形的证明方法可证明四边形ADHE是平行四边形,由平行四边形的性质即可得到:AD∥EH.
解答 解:AD∥EH,
理由如下:
连结FH交BC于D',
∵四边形BFCH是平行四边形,
∴BD'=CD',FD'=HD'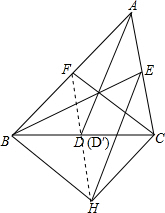
又∵D是BC中点,
∴D和D’重合,即点F、D、H共线,
∴FD=HD,
∵D、F分别是AB、BC中点,
∴DF∥AC且DF=$\frac{1}{2}$AC
∵E是AC中点,
∴DF=AE,
∴DH=AE且DH∥AE,
∴四边形ADHE是平行四边形,
∴AD∥EH.
点评 本题考查了平行四边形的判定个性质,平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
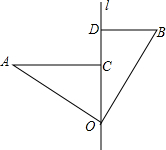 如图,点O是直线l上一点,点A、B位于直线l的两侧,且∠AOB=90°,OA=OB,分别过A、B两点作AC⊥l,交直线l于点C,BD⊥l,交直线l于点D.
如图,点O是直线l上一点,点A、B位于直线l的两侧,且∠AOB=90°,OA=OB,分别过A、B两点作AC⊥l,交直线l于点C,BD⊥l,交直线l于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com