
【题目】已知:在△ABC中,AH⊥BC,垂足为点H,若AB+BH=CH,∠ABH=70°,则∠BAC=_____°.
【答案】75°或35°
【解析】
分析题意,可知本题需分两种情况进行讨论,△ABC为锐角三角形和△ABC为直角三角形;
当△ABC为钝角三角形时,过A作BC的垂线,交CB的延长线于点H,由AB+BH=CH,不难得出AB=BC,接下来,再利用三角形外角的性质,可得∠BAC的度数;
当△ABC为锐角三角形时,在HC上取D点,使BH=HD,连接AD,再结合AB+BH=CH,不难得出AD=DC,接下来,再利用三角形外角的性质,可得∠DAC的度数;
由∠ABH=70°,利用等腰三角形的性质可得出∠BAD的度数,结合上述所得,可得∠BAC的度数.
根据题意画出图形,
当△ABC为钝角三角形时,过A作BC的垂线,交CB的延长线于点H,
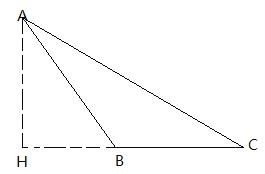
∵AB+BH=CH,HB+BC=CH,
∴AB=BC,
∴∠BAC=∠ACB.
∵∠ABH=70°,
∴∠BAC=∠ACB=35°.
当△ABC为锐角三角形时,在HC上取D点,使BH=HD,连接AD,
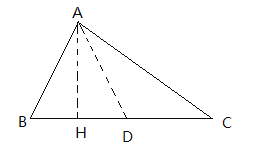
∵AB+BH=HC=HD+DC,BH=HD,
∴AB=DC.
∵AH⊥BD,BH=HD,
∴AB=AD,
∴∠B=∠ADH=70°,
∴∠BAD=40°.
∵AB=DC,AB=AD,
∴AD=CD,
∴∠C=∠DAC,
∴∠ADH=∠C+∠DAC=2∠C,
∴∠DAC=35°,
∴∠BAC=∠BAD+∠DAC=40°+35°=75°.
故答案为:75°或35°


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆, ![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.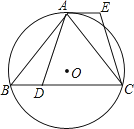
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
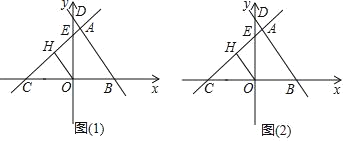
【题目】如图(1),平面直角坐标系中,直线y=![]() 与x轴、y轴分别交于点B、D,直线y=
与x轴、y轴分别交于点B、D,直线y=![]() 与x轴、y轴分别交于点C、E,且两条直线交于点A.
与x轴、y轴分别交于点C、E,且两条直线交于点A.
(1)若OH⊥CE于点H,求OH的长.
(2)求四边形ABOE的面积.
(3)如图(2),已知点F(﹣![]() ,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为(
,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为(![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C顺时针旋转60°得△ADC,连接OD.当AO=5,BO=4,α=150°时,则CO的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.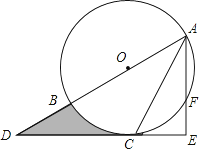
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数![]() +1的整数部分为m,小数部分为n.
+1的整数部分为m,小数部分为n.
(1)求m,n的值;
(2)在平面直角坐标系中,试判断点(m﹣1,n﹣1)位于第几象限;
(3)若m,n+1为一个直角三角形的斜边与一条直角边的长,求这个直角三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点( ![]() ,0),有下列结论:①abc>0;
,0),有下列结论:①abc>0;
②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0; ⑤a﹣b≥m(am﹣b);
其中所有正确的结论是( )
A.①②③
B.①③④
C.①②③⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在云南省某市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 
你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;扇形统计图中甲类部分的圆心是 .
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生2400人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com