
分析 利用一次项的系数分别求出常数项,把50分成9、16、25,然后与(a2-6a)、(b2-8b)、(c2-10c)分别组成完全平方公式,再利用非负数的性质,可分别求出a、b、c的值,然后利用勾股定理逆定理可证△ABC是直角三角形.
解答 解:△ABC是直角三角形
理由:∵a2+b2+c2=6a+8b+10c-50,
∴a2+b2+c2-6a-8b-10c+50=0,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形.
点评 本题主要考查了配方法的应用、勾股定理、非负数的性质,解题的关键是注意配方法的步骤,在变形的过程中不要改变式子的值.


科目:初中数学 来源: 题型:选择题
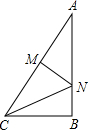 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )| A. | $\frac{35}{8}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a是实数,-a2≤0 | |
| B. | 天上打雷后就下雨 | |
| C. | 掷一枚质地均匀的硬币一次,反面朝上 | |
| D. | 某运动员跳高的最好成绩是200.1米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运动时间(秒) | 0 | 5 | 7 | t |
| A点位置 | a | -1 | ||
| B点位置 | b | 17 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com