
【题目】如图,点D在AB上,点E在AC上,AB=AC添加下列一个条件后,还不能证明△ABE≌△ACD的是( )

A.AD=AEB.BD=CEC.∠B=∠CD.BE=CD
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
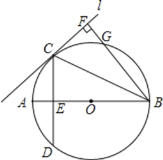
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() ,
,![]() 是实数,定义关于“*”的一种运算:
是实数,定义关于“*”的一种运算:![]() .则下列结论正确的是( )
.则下列结论正确的是( )
①若![]() ,则
,则![]() 或
或![]() ;
;
②不存在实数![]() ,
,![]() ,满足
,满足![]() ;
;
③![]() ;
;
④若![]() ,则
,则![]() .
.
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
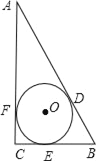
【题目】如图,在Rt△ABC中,∠C=90°,BC=5,⊙O与Rt△ABC的三边AB、BC、AC分别相切于点D、E、F,若⊙O的半径r=2,则Rt△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
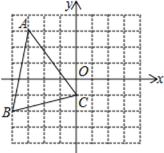
【题目】如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上
(1) 直接写出坐标:A__________,B__________
(2) 画出△ABC关于y轴的对称的△DEC(点D与点A对应)
(3) 用无刻度的直尺,运用全等的知识作出△ABC的高线BF(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
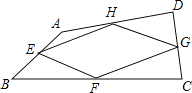
【题目】(满分8分)我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是____________;
(2)证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
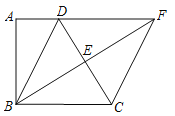
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)求证:四边形BCFD是菱形;
(2)若AD=1,BC=2,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com