练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
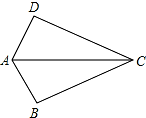
    7．如图，已知DC=BC，那么添加下列一个条件后，就能判定△ABC≌△ADC的是（　　）
    A．AD=ABB．∠BAC=∠DACC．BC=ACD．∠B=∠D=90°

    分析 由三角形全等的判定方法SSS得出AD=AB能判定△ABC≌△ADC，得出A能；B、C、D不能．

    解答 解：能判定△ABC≌△ADC的是AD=AB；理由如下：
    在△ABC和△ADC中，$\left\{\begin{array}{l}{DC=BC}&{\;}\\{AC=AC}&{\;}\\{AD=AB}&{\;}\end{array}\right.$，
    ∴△ABC≌△ADC（SSS）；
    ∠BAC=∠DAC或BC=AC或∠B=∠D判定△ABC≌△ADC条件不够；
    故选：A．

    点评 本题考查了全等三角形的判定方法；熟练掌握三角形全等的判定方法，并能进行推理论证是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

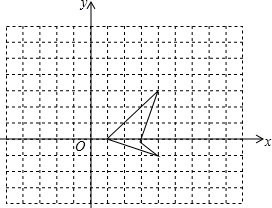    17．如图，方格纸中有一条美丽可爱的小鱼．
    （1）在同一方格纸中，画出将小鱼图案绕原点O旋转180°后得到的图案；
    （2）在同一方格纸中，在y轴的右侧，将原小鱼图案以原点O为位似中心放大，使它们的位似比为1：2，画出放大后小鱼的图案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

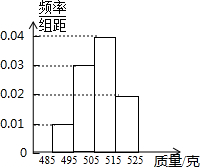    18．为了检测某自动包装流水线的生产情况，在流水线上随机抽取40件产品，分别称出它们的质量（单位：克）作为样本．如图是样本的频率分布直方图，根据图中各组的组中值估计产品的平均质量507克．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．一只小鸟自由自在地在空中飞行，然后随意落在如图所示的某个方格中（每个方格除颜色外完全一样），那么小鸟停在黑色方格中的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{5}{12}$C．$\frac{1}{3}$D．$\frac{7}{12}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，梯形ABCD中，AD∥BC，∠BAD和∠ABC的平分线相交于点E，∠BCD和∠CDA的平分线相交于点F，求证：EF∥BC∥AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．小萍要在一幅长60cm、宽40cm的风景画的四周外围，镶上一条宽度相同的金色纸边，制成一幅挂画（如图），使风景画的面积是整幅挂图面积54%．设金色纸边的宽为xcm，根据题意所列方程为（　　）
    A．（60+x）（40+x）×54%=60×40B．（60+2x）（40+2x）×54%=60×40
    C．（60+2x）（40+2x）=60×40×54%D．（60+x）（40+x）=60×40×54%

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，在△ABC中，∠CAB=90°，AB=AC，以AC为边作等边△ACD，连接BD．
    （1）求∠BDC的度数；
    （2）如图2，将△BCD沿直线BC折叠得△BCE，点D关于直线BC对称点为E，连接AE，交BD于F，交BC于G，试判断FG与GE的数量关系，并给与证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．若a=-2.6，则-a=2.6；若-b=7，则b的相反数在原点的右侧．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．在数轴上，0和-1之间表示的点的个数是（　　）
    A．0个B．1个C．2个D．无数个

    查看答案和解析>>

    同步练习册答案