[题目]如图.在4×5的网格中.最小正方形的边长为1.A.B.C.D均为格点．(1)如图1.画出所有以AB为一边且与△ABC全等的格点三角形．(2)如图2.在线段AB上画出一点P.使CP+PD最小.其最小值为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在4×5的网格中，最小正方形的边长为1，A，B，C，D均为格点（最小正方形的顶点）．

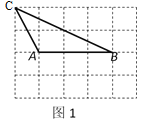
（1）如图1，画出所有以AB为一边且与△ABC全等的格点三角形．

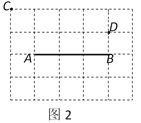
（2）如图2，在线段AB上画出一点P，使CP+PD最小，其最小值为．

【答案】（1）见解析；（2）5.

【解析】

（1）直接利用全等三角形的性质得出符合题意的三角形；

（2）．如图所示，过点D作DD’⊥AB，使DB=BD’，连接CD’，交AB于点P，则P点即为所求作.再利用勾股定理可求出结论.

（1）如图所示：

（2）如图所示，过点D作DD’⊥AB，使DB=BD’，连接CD’，交AB于点P，则P点即为所求作.

此时，CP+PD=CD’=.

故CP+PD的最小值为：5.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】△ABC 中，AB＝AC＝12 厘米，∠B＝∠C，BC＝8 厘米，点 D 为 AB 的中点．如果点 P 在线段 BC 上以 2 厘米/秒的速度由 B 点向 C 点运动，同时，点 Q 在线段 CA 上由 C 点向 A 点运动．若点 Q 的运动速度为 v 厘米/秒，则当△BPD 与△CQP 全等时，v 的值为（）

A.2B.5C.1 或 5D.2 或 3

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，如图，在平面直角坐标系中，A(-3a,0),B(0,4a)，△ABO的面积是6.

（1）求B的坐标.

（2）在x轴的正半轴上有一点C，使∠BAO=2∠BCA,AB=5,动点P从A出发，沿线段AC运动,速度为每秒1个单位长度,设点P的运动时间为t，△BCP的面积为S，用含t的式子来表示S .

（3）在(2)的条件下,在P出发的同时,Q从B出发。沿着平行于x轴的直线，以每秒2个单位长度的速度匀速向右运动，在y轴上是否存在一点R,使△PQR为以PQ为腰的等腰直角三角形，求出满足条件的t,并直接写出点R的坐标.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】拼图填空：剪裁出若干个大小.形状完全相同的直角三角形，三边长分别记为a.b.c，如图①.

（1）拼图一：分别用4张直角三角形纸片，拼成如图②③的形状，观察图②③可发现，图②中两个小正方形的面积之和（填“大于”.“小于”或“等于”）图③中小正方形的面积，用关系式表示为 .

（2）拼图二：用4张直角三角形纸片拼成如图④的形状，观察图形可以发现，图中共有个正方形，它们的面积之间的关系是，用关系式表示为 .

（3）拼图三：用8个直角三角形纸片拼成如图⑤的形状，图中3个正方形的面积之间的关系是，用关系式表示 .

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】黑板上写有1，2，3，…，2019，2020这2020个自然数，对它们进行操作，每次操作规则如下：擦掉写在黑板上的三个数后，再添写上所擦掉三个数之和的个位数字，例如：擦掉5，13和2010后，添加上8；若再擦掉8，8，38，添上4，等等.如果经过1004次操作后，发现黑板上剩下两个数，一个是29，求另一个数.