
【题目】一条公路旁依次有![]() 三个村庄,甲乙两人骑自行车分别从
三个村庄,甲乙两人骑自行车分别从![]() 村、
村、![]() 村同时出发前往
村同时出发前往![]() 村,甲乙之间的距离
村,甲乙之间的距离![]() 与骑行时间
与骑行时间![]() 之间的函数关系如图所示,下列结论:①
之间的函数关系如图所示,下列结论:①![]() 两村相距10
两村相距10![]() ;②出发1.25
;②出发1.25![]() 后两人相遇;③甲每小时比乙多骑行8
后两人相遇;③甲每小时比乙多骑行8![]() ;④相遇后,乙又骑行了15
;④相遇后,乙又骑行了15![]() 或65
或65![]() 时两人相距2
时两人相距2![]() .其中正确的个数是( )
.其中正确的个数是( )

A.1个B.2个C.3个D.4个
科目:初中数学 来源: 题型:
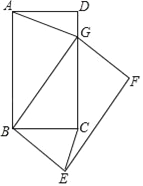
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B旋转得到矩形GBEF.
(1)观察发现:在旋转的过程中, ![]() 的值不变,这个数值是 ;
的值不变,这个数值是 ;
(2)问题解决:当点G落在直线CD上时,求CE的长;
(3)数学思考:在旋转的过程中,CE是否有最大值,如果有,请直接写出;如果没有,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠C,AD⊥BE于点F,BC⊥BE,点E,D,C在同一条直线上.
(1)判断AB与CD的位置关系,并说明理由;
(2)若∠ABC=120°,求∠BEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
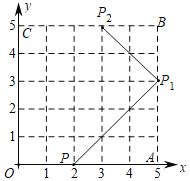
A.(5,3)B.(3,5)C.(0,2)D.(2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() .
.
(1)求反比例函数的解析式:
(2)若点![]() 为
为![]() 轴上一动点,当
轴上一动点,当![]() 是等腰三角形时,直接写出点
是等腰三角形时,直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
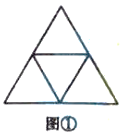
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.”小聪按此方法解关于x的方程x2+10x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为50,则该方程的正数解为( )


A.6B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.

(1)点G在BE上,且∠BDG=∠C,求证:DGCF=DMEG;
(2)在图中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com