
【题目】拼图填空:剪裁出若干个大小.形状完全相同的直角三角形,三边长分别记为a.b.c,如图①.





(1)拼图一:分别用4张直角三角形纸片,拼成如图②③的形状,观察图②③可发现,图②中两个小正方形的面积之和 (填“大于”.“小于”或“等于”)图③中小正方形的面积,用关系式表示为 .
(2)拼图二:用4张直角三角形纸片拼成如图④的形状,观察图形可以发现,图中共有 个正方形,它们的面积之间的关系是 ,用关系式表示为 .
(3)拼图三:用8个直角三角形纸片拼成如图⑤的形状,图中3个正方形的面积之间的关系是 ,用关系式表示 .
【答案】(1)等于,a2+b2=c2;(2)两个小正方形面积等于大正方形面积,a2+b2=c2;(3)三个正方形的面积差相等,(b+a)2-c2=c2-(b-a)2.
【解析】
(1)利用两图形都是两个小正方形的面积之和等于大正方形减去4个直角三角形得出,即可得出面积关系,利用直角三角形各边长度得出即可;
(2)利用图形结合直角三角形面积,可以得出两个小正方形面积相加等于大正方形面积,进而得出关系时即可;
(3)利用图形可以得出图中3个正方形的面积之间的关系为三个正方形的面积差相等,进而得出关系时即可.
解:(1)∵观察图②③可发现,图②中两个小正方形的面积之和与图③中小正方形的面积,都是两个小正方形的面积之和等于大正方形减去4个直角三角形得出,
∴图②中两个小正方形的面积之和等于图③中小正方形的面积,
∵图②中两个小正方形的面积之和为(a+b)2-2ab=a2+b2,图③中小正方形的面积为:c2,
故a2+b2=c2;
故答案为:等于,a2+b2=c2;
(2)根据图形可以得出去掉大正方形与两小正方形重叠部分,正好是4个直角三角形的面积,
故图中3个正方形的面积之间的关系是:两个小正方形面积等于大正方形面积,
用关系式表示为:a2+b2=c2;
故答案为:两个小正方形面积等于大正方形面积,a2+b2=c2;
(3)利用图形可以得出:大正方形面积-中正方形面积=中正方形面积-小正方形面积,即图中3个正方形的面积之间的关系是:三个正方形的面积差相等;
用关系式表示为:(b+a)2-c2=c2-(b-a)2.
故答案为:三个正方形的面积差相等,(b+a)2-c2=c2-(b-a)2.


科目:初中数学 来源: 题型:
【题目】一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米.

(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
(3)当梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等时,这时梯子的顶端距地面有多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )

A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×5的网格中,最小正方形的边长为1,A,B,C,D均为格点(最小正方形的顶点).
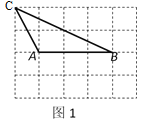
(1)如图1,画出所有以AB为一边且与△ABC全等的格点三角形.
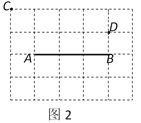
(2)如图2,在线段AB上画出一点P,使CP+PD最小,其最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com