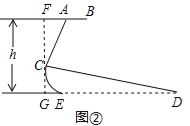
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1．6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0．8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0.1m）．
（参考数据：sin12°=cos78°≈0.21，sin68°=cos22°≈0.93，tan68°≈2.48）
【答案】1．1m．
【解析】试题分析：过C点作FG⊥AB于F，交DE于G．在Rt△ACF中，根据CF=ACsin∠CAF求出CF的长，在Rt△CDG中，根据CG=CDsin∠CDE求出CG的长，然后根据FG=FC+CG计算即可．
试题解析：解：过C点作FG⊥AB于F，交DE于G．
∵CD与地面DE的夹角∠CDE为12°，∠ACD为80°，
∴∠ACF=90°+12°﹣80°=22°，
∴∠CAF=68°，
在Rt△ACF中，CF=ACsin∠CAF≈0．744m，
在Rt△CDG中，CG=CDsin∠CDE≈0．336m，
∴FG=FC+CG≈1．1m．
故跑步机手柄的一端A的高度约为1．1m．
科目：初中数学 来源： 题型：
【题目】已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为_____秒时，△ABP和△DCE全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面的点阵图和相应的等式，探究其中的规律：
认真观察，并在
后面的横线上写出相应的等式．
；
；
；______
结合观察下列点阵图，并在
后面的横线上写出相应的等式．
；
；
；
；______
若在中的第n个点阵图斜线的左上方共有36个点，试求第n个点阵图中总共有多少个点．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点B为第一象限内一点，点A为x轴正半轴上一点，分别连接OB，AB，△AOB为等边三角形，点B的横坐标为4．
（1）如图1，求线段OA的长；
（2）如图2，点M在线段OA上（点M不与点O、点A重合），点N在线段BA的延长线上，连接MB，MN，BM＝MN，设OM的长为t，BN的长为d，求d与t的关系式（不要求写出t的取值范围）；
（3）在（2）的条件下，点D为第四象限内一点，分别连接OD，MD，ND，△MND为等边三角形，线段MA的垂直平分线交OD的延长线于点E，交MA于点H，连接AE，交ND于点F，连接MF，若MF＝AM+
AN，求点E的横坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】拼图填空：剪裁出若干个大小.形状完全相同的直角三角形，三边长分别记为a.b.c，如图①.
（1）拼图一：分别用4张直角三角形纸片，拼成如图②③的形状，观察图②③可发现，图②中两个小正方形的面积之和 （填“大于”.“小于”或“等于”）图③中小正方形的面积，用关系式表示为 .
（2）拼图二：用4张直角三角形纸片拼成如图④的形状，观察图形可以发现，图中共有 个正方形，它们的面积之间的关系是 ，用关系式表示为 .
（3）拼图三：用8个直角三角形纸片拼成如图⑤的形状，图中3个正方形的面积之间的关系是 ，用关系式表示 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销 x 件，已知产销两种产品的有关信息 如下：
产品 | 每件售价/万元 | 每件成本/万元 | 年最大产销量/件 |
甲 | 6 | 3 | 200 |
乙 | 20 | 10 | 80 |
甲、乙两产品每年的其他费用与产销量的关系分别是： y1 kx b 和 y2 ax2 m ，它们的函数图象分别如图（1）和图（2）所示.
（1）求： y1 、 y2 的函数解析式；
（2）分别求出产销两种产品的最大利润；（利润=销售额-成本-其它费用）
（3）若通过技术改进，甲产品的每件成本降到 a 万元，乙产品的年最大产销量可以达到 110 件，其它都不变，为获得最大利润，该公式应该选择产销哪种产品？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形纸片ABCD中，∠A＝60°，折叠菱形纸片ABCD，使点C落在DP(P为AB中点)所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为( )
A. 78° B. 45° C. 60° D. 75°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，
，
动点M从A点出发，以
的速度沿线段AB向点B运动，动点N从B点出发，以
的速度沿线段BC向点C运动；点M与点N同时出发，且当M点运动到B点时，M，N两点同时停止运动设点M的运动时间为
，连接MN，将
沿MN折叠，使点B落在点
处，得到
，若
，则t的值为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，Rt△ABC≌Rt△DFE，其中∠ACB＝∠DFE＝90°，BC＝EF．
(1)若两个三角形按图2方式放置，AC、DF交于点O，连接AD、BO，则AF与CD的数量关系为 ，BO与AD的位置关系为 ；
(2)若两个三角形按图3方式放置，其中C、B(D)、F在一条直线上，连接AE，M为AE中点，连接FM、CM．探究线段FM与CM之间的关系，并证明；
(3)若两个三角形按图4方式放置，其中B、C(D)、F在一条直线上，点G、H分别为FC、AC的中点，连接GH、BE交于点K，求证：BK＝EK．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com