
【题目】在平面直角坐标系中,点B为第一象限内一点,点A为x轴正半轴上一点,分别连接OB,AB,△AOB为等边三角形,点B的横坐标为4.

(1)如图1,求线段OA的长;
(2)如图2,点M在线段OA上(点M不与点O、点A重合),点N在线段BA的延长线上,连接MB,MN,BM=MN,设OM的长为t,BN的长为d,求d与t的关系式(不要求写出t的取值范围);
(3)在(2)的条件下,点D为第四象限内一点,分别连接OD,MD,ND,△MND为等边三角形,线段MA的垂直平分线交OD的延长线于点E,交MA于点H,连接AE,交ND于点F,连接MF,若MF=AM+![]() AN,求点E的横坐标.
AN,求点E的横坐标.
【答案】(1)8;(2)d=8+t;(3)点E的横坐标为6.
【解析】
(1)过点B作BH⊥OA于点H,根据等边三角形的性质解答即可;
(2)过点M作MP⊥AB于点P,根据等边三角形的性质解答即可;
(3)过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,通过等边三角形的性质和全等三角形的性质的到AN=t,OM=t,AH=MH=![]() ,OH=OM+MH=
,OH=OM+MH=![]() ,通过证明AM=AN,可得关于t的方程,求出t,即可得出答案。
,通过证明AM=AN,可得关于t的方程,求出t,即可得出答案。
解:(1)如图,过点B作BH⊥OA于点H,
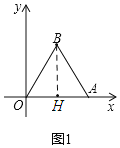
∵△AOB为等边三角形,∴BO=BA,
∵BH⊥OA,∴OH=AH,
∵点B横坐标为4,∴OH=4,
∴OA=2HO=8;
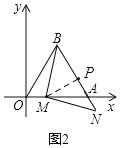
(2)如图,过点M作MP⊥AB于点P,∴∠MPA=90°,
∵BM=MN,∴BP=PN,
∵△AOB为等边三角形,∴BA=AO=8,∠BAO=60°,
∴∠AMP=30°,∴AP=![]() AM,
AM,
∵AM=8﹣t,∴AP=![]() (8﹣t)=4﹣
(8﹣t)=4﹣![]() t,∴BP=AB﹣AP=4+
t,∴BP=AB﹣AP=4+![]() t,
t,
∴BN=2BP=8+t,∴d=8+t
(3)过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,
∵△AOB为等边三角形,∴∠BOA=60°=∠OAB,
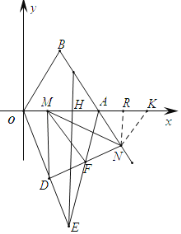
∵NK∥OB,∴∠NKA=∠BOA=60°,且∠OAB=∠NAK=60°,
∴∠NAK=∠NKA=60°,∴△AKN是等边三角形
∴AN=NK=AK,
∵△MND为等边三角形,
∴∠NMD=∠MND=60°,MN=MD,
∴∠OMD+∠NMK=∠NMK+∠MNK=180°﹣60°=120°,
∴∠OMD=∠MNK,
∵AN=8+t﹣8=t,OM=t,
∴OM=AN=NK=AK=t,且∠OMD=∠MNK,MD=MN,
∴△OMD≌△KNM (SAS),
∴OD=MK,∠MOD=∠MKN=60°,
∵MK=﹣t+t=8,∴OD=8,
∵EH垂直平分MA,∴AH=MH=![]() AM=
AM=![]() (8﹣t)=4﹣
(8﹣t)=4﹣![]() t,
t,
∴OH=OM+MH=t+4﹣![]() t=4+
t=4+![]() t,
t,
∵∠OEH=90°﹣60°=30°,∴OE=2HO=8+t,∴DE=8+t﹣8=t,∴DE=AN,
∵∠DOA=∠BAO,∴BN∥OE,∴∠NAF=∠DEF,
又∵∠AFN=∠EFD,AN=DE,∴△AFN≌△EFD(AAS),∴FN=FD,
又∵MN=MD,∴MF⊥DN,
∵NR⊥AK,∴∠ARN=90°,且∠NAK=60°,∴∠ANR=30°,
∴AR=![]() ,
,
∵MR=AM+AR=AM+![]() ,MF=AM+
,MF=AM+![]() ,∴MR=MF,且 MF⊥DN,NR⊥AK,
,∴MR=MF,且 MF⊥DN,NR⊥AK,
∴∠MNR=∠MND=60°,∴∠NMA=90°﹣60°=30°,
∵∠BAO=∠AMN+∠ANM,∴∠AMN=∠ANM=30°,∴AM=AN,∴8﹣t=t,∴t=4,
∴OH=4+![]() ×4=6,∴点E的横坐标为6.
×4=6,∴点E的横坐标为6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC>BA,AD=DC,

(1)若BD⊥CD,∠C=60°,BC=10,求AD的长;
(2)若BD平分∠ABC,求证:∠A+∠C=180°。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
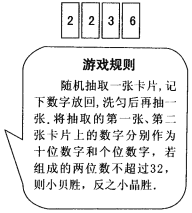
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:一个点将一条直线分为两段,如果其中较长的一段与整个线段的比等于较短一段与较长一段的比,我们就说这个点是这条线段的黄金分割点,较长的一段与整个线段的比值![]() 或较短一段与较长一段的比值
或较短一段与较长一段的比值![]() 叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是
叫做黄金分割数,用一元二次方程的知识可以求出黄金分割数是![]() 我国国旗上的正五角星中就存在黄金分割点
我国国旗上的正五角星中就存在黄金分割点![]() 解决问题:
解决问题:
![]() 如图,已知A、B、C、D、E是
如图,已知A、B、C、D、E是![]() 的五等分点,求
的五等分点,求![]() 的度数;
的度数;
![]() 若AC、AD分别与BE交于点M、
若AC、AD分别与BE交于点M、![]() 求证:点M是线段BN的一个黄金分割点.
求证:点M是线段BN的一个黄金分割点.
![]() 若
若![]() ,则
,则![]() ______
______![]() 若有根号保留根号
若有根号保留根号![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米.

(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
(3)当梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等时,这时梯子的顶端距地面有多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示为一个无盖的正方体纸盒,现将其展开成平面图,如图(2)所示.已知展开图中每个正方形的边长为1:

(1)在展开图(2)中可画出最长线段的长度为 ,在平面展开图(2)中这样的最长线段一共能画出 条。
(2)试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校课程安排中,各班每天下午只安排三节课.
(1)初一(1)班星期二下午安排了数学、英语、生物课各一节,通过画树状图求出把数学课安排在最后一节的概率;
(2)星期三下午,初二(1)班安排了数学、物理、政治课各一节,初二(2)班安排了数学、语文、地理课各一节,此时两班这六节课的每一种课表排法出现的概率是![]() .已知这两个班的数学课都由同一个老师担任,其他课由另外四位老师担任.求这两个班数学课不相冲突的概率.
.已知这两个班的数学课都由同一个老师担任,其他课由另外四位老师担任.求这两个班数学课不相冲突的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com