
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;
②当x= ![]() 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确结论是 . (填序号)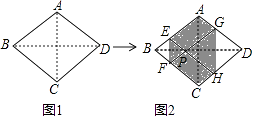
【答案】①④
【解析】解:∵菱形ABCD的边长为2,
∴AB=BC=2,
∵∠ABC=60°,
∴AC=AB=2,BD=2 ![]() ,
,
由折叠知,△BEF是等边三角形,
当x=1时,则AE=1,
∴BE=AB﹣AE=1,
由折叠知,BP=2× ![]() =
= ![]() =
= ![]() BD,
BD,
∴点P是菱形ABCD的对角线的交点,
即:点P是菱形ABCD的中心,所以①正确,
如图,
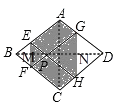
∵AE=x,
∴BE=AB﹣AE=2﹣x,
∵△BEF是等边三角形,
∴EF=BE=2﹣x,
∴BM= ![]() EM=
EM= ![]() ×
× ![]() EF=
EF= ![]() (2﹣x),
(2﹣x),
∴BP=2BM= ![]() (2﹣x),
(2﹣x),
∴DP=BD﹣BP=2 ![]() ﹣
﹣ ![]() (2﹣x)=
(2﹣x)= ![]() x,
x,
∴DN= ![]() DP=
DP= ![]() x,
x,
∴GH=2GN=2× ![]() x=x,
x=x,
当x= ![]() 时,AE=
时,AE= ![]() ,
,
∴BE=AB﹣AE= ![]() ,
,
∵△BEF是等边三角形,
∴EF=BE= ![]() ,BP=
,BP= ![]() ,
,
∴DP= ![]() ,
,
∴GH=DG= ![]() ,
,
∴EF+GH=2=AC,所以②错误;
当0<x<2时,
∵AE=x,
∴BE=2﹣x,
∴EF=2﹣x,
∴BP= ![]() (2﹣x),
(2﹣x),
∴DP= ![]() x,
x,
∴GH=2× ![]() =x=DG=DH,
=x=DG=DH,
∴六边形AEFCHG面积=S菱形ABCD﹣S△BEEF﹣S△DGH
= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]() (2﹣x)2﹣
(2﹣x)2﹣ ![]() x2
x2
=2 ![]() ﹣
﹣ ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]()
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴当x=1时,六边形AEFCHG面积最大为 ![]() ,所以③错误,
,所以③错误,
六边形AEFCHG周长=AE+EF+FC+CH+HG+AG
=x+2﹣x+x+2﹣x+x+2﹣x=6是定值,
所以④正确,即:正确的有①④,
所以答案是①④.
【考点精析】关于本题考查的二次函数的最值和菱形的性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】一副直角三角尺叠放如图 1 所示,现将 45°的三角尺ADE 固定不动,将含 30°的三角尺 ABC 绕顶点 A 顺时针转动(旋转角不超过 180 度),使两块三角尺至少有一组边互相平行.如图 2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用格点和三角尺画图:
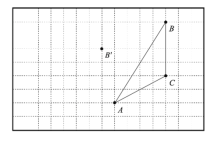
(1)补全△A′B′C′;
(2)请在AC边上找一点D,使得线段BD平分△ABC的面积,在图上作出线段BD;
(3)利用格点在图中画出AC边上的高线BE;
(4)求△ABD的面积_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设M(m,n)在反比例函数y=﹣ ![]() 上,其中m是分式方程
上,其中m是分式方程 ![]() ﹣1=
﹣1= ![]() 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A.y=﹣ ![]() x﹣
x﹣ ![]()
B.y= ![]() x+
x+ ![]()
C.y=4x﹣5
D.y=﹣4x+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,全程800km;所行的路程与时间的函数图像如图所示,下列问题:①乙车比甲车早出发2h;②甲车追上乙车时行驶了300km;③乙车的速度小于甲车速度;④甲车跑完全程比乙车跑完全程少用3h;以上正确的序号是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题 1、如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种)
2、
(1)如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种).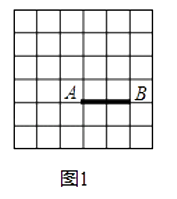
(2)如图2,在Rt△DEF中,∠DEF=90°,DE=1,sin∠F= ![]() .用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.
.用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.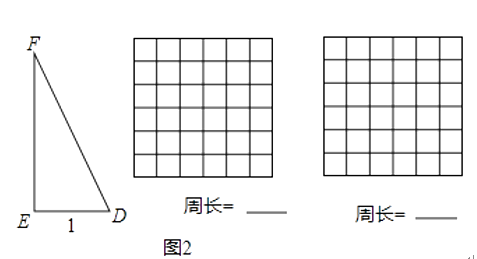
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(或方程组)解应用题:
(1)某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?
(2)某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2﹣ab﹣bc﹣ac=![]() [(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.
[(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁、美观.
(1)请你检验说明这个等式的正确性.
(2)若a=2019,b=2020,c=2021,你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值吗?
(3)若a﹣b=![]() ,b﹣c=
,b﹣c=![]() ,且a2+b2+c2=1,求ab+bc+ac的值.
,且a2+b2+c2=1,求ab+bc+ac的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D
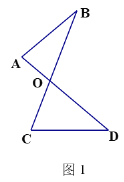
(简单应用)
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=28°,∠ADC=20°,求∠P的度数(可直接使用问题(1)中的结论)
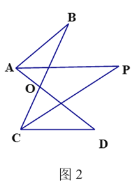
(问题探究)
(3)如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,若∠A=30°,∠C=18°,则∠P的度数为
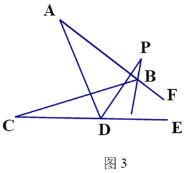
(拓展延伸)
(4)在图4中,若设∠C=x,∠B=y,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P)
∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P)
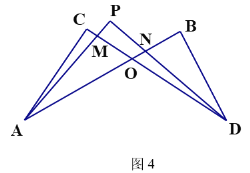
(5)在图5中,BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论 .
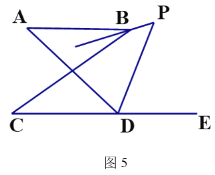
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com