
【题目】(问题背景)
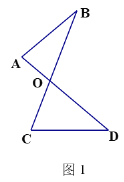
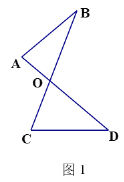
(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D
(简单应用)
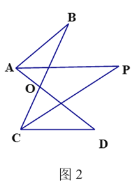
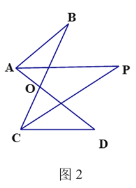
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=28°,∠ADC=20°,求∠P的度数(可直接使用问题(1)中的结论)
(问题探究)
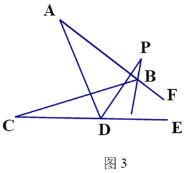
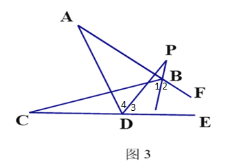
(3)如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,若∠A=30°,∠C=18°,则∠P的度数为
(拓展延伸)
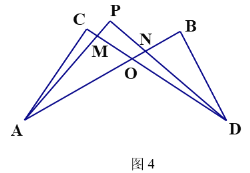
(4)在图4中,若设∠C=x,∠B=y,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P)
∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P)
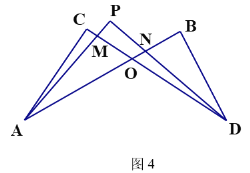
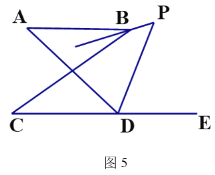
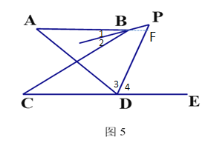
(5)在图5中,BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论 .
【答案】(1)证明见解析;(2)24°;(3)24°;(4)∠P=![]() x+
x+![]() y;(5)∠P=
y;(5)∠P=![]()
【解析】
(1)根据三角形内角和为180°,对顶角相等,即可证得∠A+∠B=∠C+∠D
(2)由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC①,∠PAD+∠P=∠PCD+∠ADC②,将两个式子相加,已知AP、CP分别平分∠BAD、∠BCD,可得∠BAP=∠PAD,∠BCP=∠PCD,可证得∠P=![]() (∠ABC+∠ADC),即可求出∠P度数.
(∠ABC+∠ADC),即可求出∠P度数.
(3)已知直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,可得∠1=∠2,∠3=∠4,由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1,∠A+∠4=∠P+∠2,两式相加即可求出∠P的度数.
(4)由(1)的结论得:![]() ∠CAB+∠C=∠P+
∠CAB+∠C=∠P+![]() ∠CDB,
∠CDB,![]() ∠CAB+∠P=∠B+
∠CAB+∠P=∠B+![]() ∠CDB,第一个式子乘以3,得到的式子减去第二个式子即可得出用x、y表示∠P
∠CDB,第一个式子乘以3,得到的式子减去第二个式子即可得出用x、y表示∠P
(5)延长AB交DP于点F,标注出∠1,∠2,∠3,∠4,由(1)的结论得:∠A+2∠1=∠C+180°-2∠3,其中根据对顶角相等,三角形内角和,以及外角的性质即可得到∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P,代入∠A+2∠1=∠C+180°-2∠3,即可得出∠P与∠A、∠C的关系.
(1)如图1,
∠A+∠B+∠AOB=∠C+∠D+∠COD=180°
∵∠AOB=∠COD
∴∠A+∠B=∠C+∠D
(2)∵AP、CP分别平分∠BAD、∠BCD
∴∠BAP=∠PAD,∠BCP=∠PCD,
由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC①,∠PAD+∠P=∠PCD+∠ADC②
①+②,得2∠P+∠PAD+∠BCP=∠BAP+∠ABC +∠PCD+∠ADC
∴∠P=![]() (∠ABC+∠ADC)
(∠ABC+∠ADC)
∴∠ABC=28°,∠ADC=20°
∴∠P=![]() (28°+20°)
(28°+20°)
∴∠P=24°
故答案为:24°
(3)∵如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,
∴∠1=∠2,∠3=∠4
由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1①,∠A+∠4=∠P+∠2②
①+②,得∠C+180°-∠3+∠A+∠4=∠P+180°-∠1+∠P+∠2
∴30°+18°=2∠P
∴∠P=24°
故答案为:24°
(4)由(1)的结论得:![]() ∠CAB+∠C=∠P+
∠CAB+∠C=∠P+![]() ∠CDB①,
∠CDB①,![]() ∠CAB+∠P=∠B+
∠CAB+∠P=∠B+![]() ∠CDB②
∠CDB②
①×3,得![]() ∠CAB+3∠C=3∠P+
∠CAB+3∠C=3∠P+![]() ∠CDB③
∠CDB③
②-③,得∠P-3x=y-3∠P
∴∠P=![]() x+
x+![]() y
y
故答案为:∠P=![]() x+
x+![]() y
y
(5)如图5所示,延长AB交DP于点F
由(1)的结论得:∠A+2∠1=∠C+180°-2∠3
∵∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P
∴∠A+360°-2∠A-2∠3-2∠P=∠C+180°-2∠3
解得:∠P=![]()
故答案为:∠P=![]()


科目:初中数学 来源: 题型:
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;
②当x= ![]() 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确结论是 . (填序号)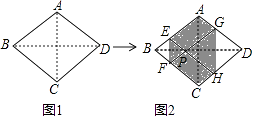
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.

(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com