
����Ŀ����һ�������Ŀڴ���װ�зֱ��������1��2��3��4�ĸ�С�����ֲ�ͬ�⣬С��û���κ�����ÿ��ʵ���Ƚ�����ȣ�
��1����������ȡһ�����ϵ�����Ϊż���ĸ���Ϊ���٣�
��2����������ȡһ���Żأ����ٴ�����ȡһ�����û���״ͼ���б���ķ�������������ϵ�����֮��Ϊż���ĸ��ʣ�
��3�������һ����Ϸ������������ȡ�����������ϵ�����֮��ľ���ֵΪ1Ϊ��ʤ������Ϊ��ʤ������������Ϸ������ƶԼס���˫����ƽ��˵�����ɣ�
���𰸡�
��1���⣺�߲����Ŀڴ���װ�зֱ��������1��2��3��4�ĸ�С�����ϵ�����Ϊż������2��4��
�������ȡһ�����ϵ�����Ϊż���ĸ���Ϊ�� ![]() =
= ![]()
��2���⣺����״ͼ�ã�
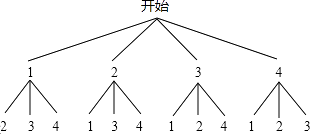
�߹���12�ֵȿ��ܵĽ�����������ϵ�����֮��Ϊż�����У�1��3������2��4������3��1������4��2����4�������
���������ϵ�����֮��Ϊż���ĸ���Ϊ�� ![]() =
= ![]()
��3���⣺���������ϵ�����֮��ľ���ֵΪ1���У�1��2������2��3������2��1������3��2������3��4������4��3����6�������
��P����ʤ��= ![]() ��P����ʤ��=
��P����ʤ��= ![]() ��
��
��P����ʤ��=P����ʤ����
��������Ϸ������ƶԼס���˫����ƽ
����������1���ɲ����Ŀڴ���װ�зֱ��������1��2��3��4�ĸ�С�����ϵ�����Ϊż������2��4�����ø��ʹ�ʽ������ô𰸣���2�����Ȼ�����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ�����������ϵ�����֮��Ϊż������������ø��ʹ�ʽ������ô𰸣���3���ֱ���ü�ʤ����ʤ�ĸ��ʣ��Ƚϸ��ʣ����ɵó����ۣ�


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵ��������Σ�AB=AC��
��1���������Σ���ͼ1����DE��BCʱ����DBEC�������������������=����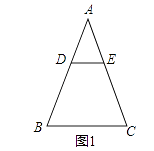
��2������̽��������ͼ1�еġ�ADE�Ƶ�A˳ʱ����ת����0�㣼����180�㣩��ͼ2λ�ã���1���еĽ��ۻ��������������������֤����������������˵�����ɣ�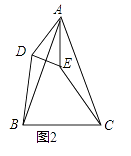
��3����չ���ã���ͼ3��P�ǵ���ֱ��������ABC��һ�㣬��ACB=90�㣬��PB=1��PC=2��PA=3�����BPC�Ķ�����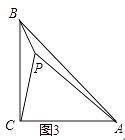
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
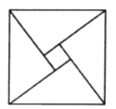
����Ŀ��2002��8���ڱ����ٿ��Ĺ�����ѧ�Ҵ����ȡ�����ҹ��Ŵ���ѧ����ˬ�ġ�����Բ��ͼ�����������ĸ�ȫ�ȵ�ֱ�����������м��С������ƴ�ɵ�һ����������(��ͼ).����������ε������100��С�����ε������4��ֱ�������ν϶̵�ֱ�DZ߳�Ϊ![]() ���ϳ���ֱ�DZ߳�Ϊ
���ϳ���ֱ�DZ߳�Ϊ![]() ����ô
����ô![]() ��ֵ��_________.
��ֵ��_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD����AB��CD��E��F��AD�����㣬CE��AD��BF��AD����CE��a��BF��b��EF��c����AD�ij�Ϊ�� ��
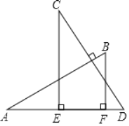
A. a+cB. b+cC. a��b+cD. a+b��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA���O�����ڵ�A����AB��OP������ΪC��OP���O�ཻ��D�㣬��֪OP=4����OPA=30�㣮��OC��AB�ij��� 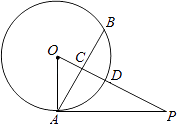
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�ı�AB��x���ϣ���ABC=90�㣬AB=BC��OA=1��OB=4��������y=x2+bx+c����A��C���㣮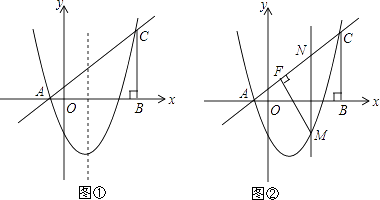
��1���������ߵĽ���ʽ���䶥�����ꣻ
��2����ͼ�٣���P����������λ��x���·���һ�㣬��Q���P���������ߵĶԳ���Գƣ�����P��Q�ֱ���x�������ߣ�����Ϊ��D��E���Ǿ���DPQE���ܳ�Ϊd����d�����ֵ�������ʹd���ֵʱ��P�����ꣻ
��3����ͼ�ڣ���M����������λ��ֱ��AC�·���һ�㣬����M��MF��AC�ڵ�F������MC����MN��BC��ֱ��AC�ڵ�N����MN����MFC������ֳ�2��3�����֣���ȷ��M������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�P�ǶԽ���BD��һ�㣬����AP��![]() ��BF��AP��H��CP��BH�ӳ��߷ֱ�AD���ڵ�E��F��
��BF��AP��H��CP��BH�ӳ��߷ֱ�AD���ڵ�E��F��
��1����֤����DAP=��DCE
��2����֤��AE=FD
��3�������APE���FBD��������ϵ����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ֽƬABCD�У���֪AB=6��BC=8��E�DZ�AD�ϵĵ㣬��CEΪ�ۺ��۵�ֽƬ��ʹ��D���ڵ�F��������FC������AEFΪֱ��������ʱ��DE�ij�Ϊ________.
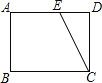
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC=90�㣬AB=BC��BD��AC�ڵ�D��CEƽ����ACB����AB�ڵ�E����BD�ڵ�F��
��1����֤����BEF�ǵ��������Σ�
��2����֤��BD=![]() ��BC+BF����
��BC+BF����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com